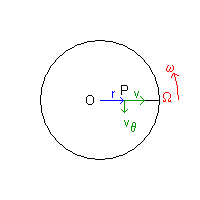
fig. 1
(note a cura di Roberto Bigoni)
In un sistema inerziale I di origine O una particella P di massa m in un certo istante si muove con velocità costante v verso un osservatore Ω che ruota attorno a O con velocità angolare costante ω. Per Ω, P apparirà dotata non solo di una componente radiale della velocità, ma anche di una componente perpendicolare alla direzione OP, tanto più intensa quanto maggiore è la distanza r = OP.

fig. 1
Se si indica con ur il versore radiale OP e con uθ il versore tangenziale, perpendicolare a ur, per Ω la velocità istantanea della particella è descritta dal vettore
![]()
Per Ω, P si sta avvicinando; lo scalare ω va considerato positivo se la rotazione è antioraria, negativo in caso contrario.
Poiché la distanza r non è costante, vΩ non è costante e quindi il punto appare dotato di una accelerazione data dalla derivata rispetto al tempo di vΩ.
Derivando vΩ rispetto al tempo, sempre nel caso particolare considerato in cui i moduli v e ω sono costanti, applicando la regola di derivazione dei prodotti, si ottiene
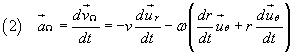
Per calcolare le derivate rispetto al tempo dei versori ur e uθ, ricordando che, per definizione, i versori hanno modulo 1, si può osservare che
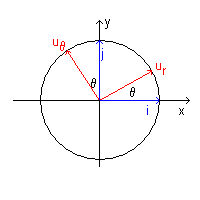
fig. 2
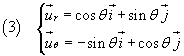
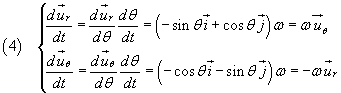
Sostituendo nella (2) i valori delle derivate dei versori ottenute nelle (4)
e osservando che
![]() , si ha
, si ha
![]()
![]()
Per il secondo principio della dinamica, questa accelerazione implica la presenza due forze acceleranti, una radiale
![]()
e una tangenziale
![]()
Un'espressione più generale della (8) può essere ottenuta descrivendo la velocità angolare come un vettore di modulo ω perpendicolare al piano dei versori ur e uθ e verso uscente dal piano se la rotazione è antioraria, entrante nel caso contrario. Con il simbolismo del prodotto vettoriale si ha
![]()
Queste forze non sono originate da nessuna interazione reale tra la particella P e altre particelle.
Le interazioni reali sono quelle riconducibili a una delle quattro interazioni fondamentali identificate dai fisici da Newton in poi:
Queste forze sono quindi classificate come forze fittizie e, per il fatto che in Ω si manifestano forze fittizie, Ω è un sistema non inerziale.
La forza (7) è denominata forza centrifuga. In Ω un punto che nel sistema inerziale I ha velocità costante (eventualmente anche nulla) appare spinto ad allontanarsi dal polo O.
La forza (8) è denominata forza di Coriolis dal nome del fisico francese Gaspard Gustave de Coriolis che per primo ne evidenziò gli effetti. In Ω il punto appare sottoposto ad una spinta laterale che lo fa deflettere da una traiettoria rettilinea. Poiché la spinta è perpendicolare alla componente radiale della velocità, la spinta si comporta istante per istante come una forza centripeta che costringe il punto a ruotare su un arco di circonferenza.
Se si interpreta la fig.1

fig. 1
come la rappresentazione dell'emisfero terrestre boreale visto da un punto sovrastante il polo nord O e P come una massa fluida (aria o acqua) diretta, in un certo istante, a sud verso un punto Ω sull'equatore, a causa della rotazione terrestre attorno all'asse passante per i poli, un osservatore terrestre vedrà deflettere la corrente verso ovest con una rotazione in senso orario. Un fluido che invece si muovesse dall'equatore verso il polo defletterà verso est, sempre con una rotazione oraria. Nell'emisfero australe la rotazione delle correnti è invece antioraria. Si veda, ad esempio, lo schema delle principali correnti oceaniche nella pagina NOS Education.
La seguente applicazione Javascript calcola la traiettoria di un proiettile (in assenza di gravità)
vista da un sistema rotante con origine Ω.
Nell'istante iniziale il proiettile ha posizione P(x0;y0) e velocità costante di componenti vx
e vy.
Il sistema rotante, rispetto ad un sistema inerziale, ha velocità angolare ω
positiva se la rotazione è antioraria, negativa in caso contrario.
La seguente applicazione calcola la traiettoria della massa puntiforme di un pendolo ideale in un sistema con origine Ω in
rotazione con velocità angolare ω rispetto ad un sistema inerziale.
Nell'istante iniziale il pendolo, lungo l, si trova in Ω e ha velocità radiale v0 di intensità massima
con direzione coincidente con l'asse x.
I valori di default evidenziano il fenomeno noto come
pendolo di Foucault: il piano
di oscillazione, costante in un sistema inerziale, appare ruotare attorno all'origine Ω.
ultima revisione: Maggio 2018