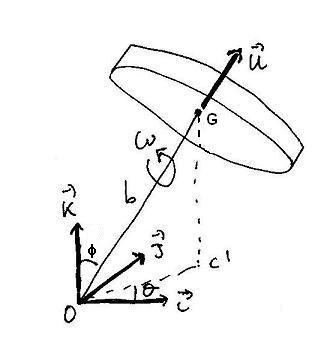
Un disco rigido di massa m, con raggio molto grande rispetto al suo spessore, ruota in senso antiorario con velocità angolare costante ω attorno ad un perno rigido OG di massa trascurabile, di lunghezza b, saldato al suo baricentro G, perpendicolare al suo piano e vincolato senza attriti al punto fisso O.
Se il corpo ha momento di inerzia I rispetto all'asse di rotazione, il suo momento angolare s,
che sarà indicato come momento angolare di spin,
ha modulo 
.
Indicando con u il versore dell'asse di rotazione, con i, j e k i versori degli assi del sistema di riferimento del laboratorio, con φ l'angolo che u forma con k e con θ l'angolo che la proiezione di u sul piano ij forma con i si ha
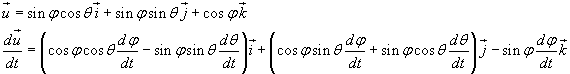
e quindi
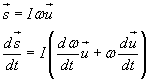
Se ω è costante si ha
Indicando con il vettore b la posizione di G rispetto a O si ha inoltre
Sul baricentro G agisce la forza peso 
:
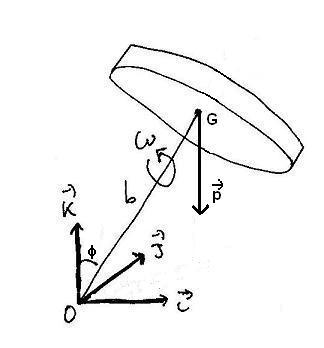
Il momento torcente del peso τ è quindi
Dai principi della meccanica rotazionale si ha
Se l'angolo φ è nullo anche τ è nullo; la derivata del momento angolare rispetto al tempo è nulla; il momento angolare è costantemente
Per angoli φ > 0 (e ovviamente minori di un angolo piatto) si ha
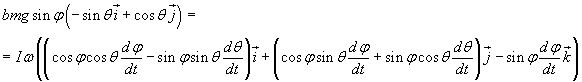
La componente nel verso k a secondo membro deve essere nulla. Quindi
cioè l'angolo φ è costante. Uguagliando le altre due componenti risulta
L'asse di rotazione del corpo, cioè il versore u, ruota a sua volta attorno al versore k con velocità angolare di modulo costante
.
Tale velocità angolare è detta velocità angolare di precessione ed è rappresentata vettorialmente da
.
Tale comportamento è evidenziato nei giroscopi e sfruttato in numerose applicazioni.
Un giroscopio in You Tube.
Esempio
Un disco di massa 
e
raggio 
ruota attorno al suo asse
con frequenza 
su un perno
lungo 
.
Ricordando che il momento di inerzia I del disco è
, si ottiene
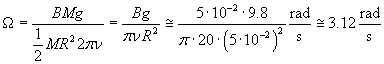
Con φ costante e
,
il versore u e la sua derivata rispetto al tempo del risultano
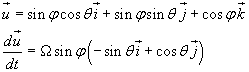
Si ha quindi
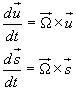
Ma la presenza della velocità angolare di precessione significa che il disco, oltre a ruotare sul proprio asse di
simmetria u, in un tempo 
compie una rotazione completa anche attorno all'asse k. Quindi al momento angolare di spin va aggiunto il
momento angolare dovuto a questa rotazione.
Questa correzione può essere trascurabile se Ω è molto piccolo, cioè se il prodotto Iω è molto grande, ma in caso contrario implica conseguenze notevoli sulla meccanica del disco, dando luogo al fenomeno detto nutazione.
Detto Ik il momento d'inerzia del disco rispetto all'asse k, il contributo al momento angolare totale L di questa rotazione risulta
e il momento angolare totale L è quindi
Derivando rispetto al tempo si ottiene
Quindi la velocità angolare di precessione Ω in effetti non riguarda il vettore s, cioè il momento angolare di spin, ma il vettore L del momento angolare totale: è L che ruota attorno all'asse k con velocità angolare costante Ω mentre s a sua volta ruota attorno a L con velocità angolare ω.
Di conseguenza, detto φ0 l'angolo costante che L forma con il versore k, detto φ l'angolo tra s e k e detto α il massimo scostamento angolare di φ da φ0, φ oscilla sinusoidalmente nel tempo con pulsazione ω.
Con una opportuna scelta dell'istante iniziale si ha
ultimo aggiornamento: 31/01/2020