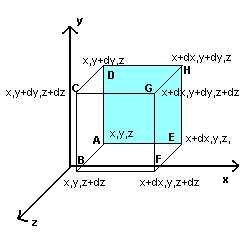
Riferendosi alla figura, la circuitazione di un campo vettoriale h lungo i lati del quadrato AEHD, parallelo al piano (x,y), è data da
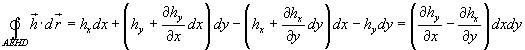
Questo risultato può essere interpretato come il risultato del prodotto scalare tra un vettore R tale che
e il vettore dxdyk perpendicolare al piano xy e diretto come l'asse z.
Rappresenta quindi il flusso del vettore R
attraverso la superficie di contorno AEHD.
Ragionamenti analoghi sui quadrati ABCD e ABFE portano alle seguenti conclusioni:
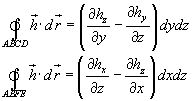
Data una generica superficie dS, il vettore normale ad essa e di modulo dato dalla sua area è
La circuitazione dΓh di h lungo il contorno dσ di dS è data dalla somma delle circuitazioni attorno ai contorni delle componenti di dS, cioè delle sue proiezioni sui piani definiti dagli assi cartesiani:
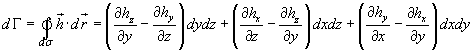
Questo risultato può essere interpretato come il prodotto scalare tra il vettore
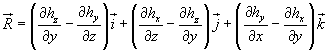
e il vettore 
,
cioè come il flusso dΦR di R per la superficie dS.
A sua volta, il vettore R può essere interpretato come il prodotto vettoriale
di 
per h:
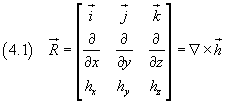
In generale il prodotto vettoriale di
per h è detto
rotore di h. Quindi R è il rotore di h.
In conclusione si può affermare che
la circuitazione dΓ di un campo vettoriale h lungo il contorno dσ di una superficie dS è uguale al flusso dΦR del rotore di h attraverso la superficie dS:
Questo risultato è noto come Teorema di Stokes.
Una conseguenza immediata di questo teorema è che un campo è conservativo se e solo se il suo rotore è nullo.
Se h rappresenta un campo elettrico E, per la legge di Faraday, la circuitazione di E è uguale alla derivata rispetto al tempo del flusso di induzione magnetica B
Uguagliando i secondi membri di (4.2) e (4.3) si ottiene
La (4.4) è una delle equazioni di Maxwell.
Se invece h rappresenta un campo di induzione magnetica B, per la legge di Ampère-Maxwell, la circuitazione di B è data da
dove I rappresenta la corrente concatenata con il percorso di circuitazione dσ e può essere espressa come flusso di densità di corrente J attraverso la superficie dS. Quindi
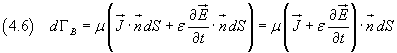
Uguagliando i secondi membri di (4.2) e (4.6) si ottiene
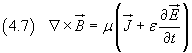
La (4.7) completa la quaterna delle
equazioni di Maxwell:
