Note a cura di Roberto Bigoni
(Nel testo le grandezze vettoriali sono denotate da lettere in grassetto; nelle formule numerate le grandezze vettoriali sono sormontate da una freccetta, il prodotto scalare è indicato con il punto · e il prodotto vettoriale è indicato dal segno ×.)

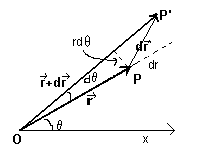
La posizione di un punto P in un piano è rappresentabile in modo biunivoco scegliendo un sistema di riferimento polare con polo in O e asse polare OX e facendo corrispondere a P un vettore r di modulo uguale alla misura del segmento OP e anomalia θ data dalla misura dell'angolo orientato XOP.
Se con una variazione infinitesima di posizione il punto P si sposta in P', alla nuova posizione corrisponde un nuovo vettore r', rappresentabile come somma vettoriale di r+dr.
dr rappresenta uno spostamento infinitesimo, che a sua volta può essere espresso come somma di due vettori infinitesimi, uno radiale, cioè diretto come OP, di modulo uguale a dr (variazione infinitesima del modulo) e uno tangenziale (perpendicolare a OP) di modulo uguale a r dθ.
Indicando con ur il versore radiale e con uθ il versore tangenziale, si può scrivere
![]()
Poiché il vettore velocità è la derivata del vettore posizione rispetto al tempo, risulta
![]()
Il primo addendo a secondo membro della (1.2) è il componente radiale della velocità o, più brevemente, la velocità radiale; il secondo addendo è il componente tangenziale della velocità o, più brevemente, la velocità tangenziale.
Con una convenzione introdotta da Newton, si indicano la derivata prima di una grandezza rispetto al tempo sovrapponendo un punto al simbolo della grandezza. Con questa notazione la (1.2) può essere scritta
![]()
Spesso inoltre si indica la derivata dell'anomalia θ rispetto al tempo, detta
velocità angolare, con il simbolo ω.
Si potrà quindi avere anche la seguente versione della (1.2)
![]()
Il quadrato del modulo della velocità risulta
![]()
Il vettore accelerazione per definizione è dato dalla derivata del vettore velocità rispetto al tempo:
![]()
allora derivando i membri della (1.2.2)
![]()
Per ottenere le derivate dei versori radiale e tangenziale è utile rappresentare questi versori in un sistema cartesiano.
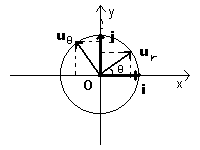
Detti i e j i versori degli assi cartesiani si ha
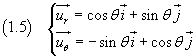
Derivando le (1.5) rispetto a θ si ha
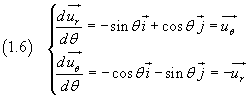
e ancora
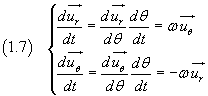
Usando le (1.7) dalla (1.4) si ha
![]()
e raccogliendo
![]()
Se il modulo della posizione è costante il moto è un moto
circolare: con centro nel polo O.
In questo caso la velocità radiale è nulla: la velocità coincide
con la velocità tangenziale.
Nel caso di un moto circolare si ha quindi
![]()
Se in un moto circolare ω è costante, il moto si dice moto circolare uniforme.
Nel moto circolare uniforme, detto T il periodo, cioè la durata di una rotazione completa,
![]()
e l'espressione dell'accelerazione della (1.9) si riduce a
![]()
cioè l'accelerazione ha solo la componente radiale, costante, diretta dal punto al polo.
L'accelerazione si dice centripeta.
Il lavoro di una forza f che provoca uno spostamento infinitesimo dr del suo punto di applicazione per definizione è
![]()
Per il secondo principio della dinamica
![]()
Allora dalla (2.1) si ricava
![]()
Differenziando il quadrato della velocità si ottiene
![]()
L'ultima espressione ottenuta nella (2.3) è quindi
![]()
dove si è posto
![]()
K è detta energia cinetica.
In definitiva dalla (2.1) si ottiene
![]()
ovvero, in forma finita,
![]()
Se un corpo (supposto puntiforme) di massa m si muove con velocità v, il suo momento cinetico (detto anche semplicemente momento o anche quantità di moto) è p=mv.
Se il corpo si trova nel punto P di posizione r rispetto al polo O, il suo momento angolare rispetto al polo O è
![]()
Derivando entrambi i membri della (3.1) rispetto al tempo si ottiene
![]()
Il primo prodotto vettoriale a secondo membro è nullo, poiché la derivata del vettore posizione è il vettore velocità che è parallelo al momento cinetico.
La derivata del momento cinetico rispetto al tempo, per il secondo principio della dinamica
![]()
è la forza che agisce sul corpo. In generale quindi
![]()
Nella (3.3) il vettore τ, prodotto vettoriale tra posizione e forza,
è detto momento della forza.
La (1.3) può essere vista come estensione del secondo principio della dinamica alle
grandezze angolari: a f corrisponde τ, a p corrisponde l e
τ è la derivata rispetto al tempo di l come f è
la derivata rispetto al tempo di p.
Se f è una forza centrale, cioè parallela a r, il suo momento è nullo; è quindi nulla anche la derivata del momento angolare rispetto al tempo, cioè il momento angolare di una forza centrale è costante.
Se un vettore è costante, sono costanti la sua direzione, il suo verso e il suo modulo.
La direzione del momento angolare, che è il prodotto vettoriale di r per
p, è perpendicolare al piano di r e p: ciò significa che
r e p, durante il movimento del corpo, sono sempre sullo stesso piano.
La traiettoria del movimento è quindi una curva piana che viene percorsa dal corpo
sempre con lo stesso senso di rotazione.
In prima approssimazione, cioè trascurando le forze dovute alla presenza degli altri pianeti, la forza di gravitazione universale ipotizzata da Newton agente su un singolo pianeta è una forza centrale diretta dal pianeta verso il Sole,
![]()
Tale legge prevede quindi che i pianeti percorrano orbite descritte da curve piane e siano privi di moto retrogrado.
Il modulo di l è rp sinδ dove con δ si indica l'angolo tra i vettori r e p.
p sinδ è quindi la componente tangenziale del momento cinetico, quindi il prodotto della massa per la velocità tangenziale.
La velocità tangenziale è ωr, quindi
![]()
ω, a sua volta, è la derivata dell'anomalia θ rispetto al tempo. Allora
![]()
r2dθ può essere interpretato geometricamente come il doppio dell'area dA spazzata dal vettore posizione nel tempo dt
![]()
In definitiva
![]()
Poiché il secondo membro è costante, è costante anche il primo membro, detto velocità areolare.
Questa è la seconda delle leggi di Keplero, da lui ricavate in base alle osservazioni astronomiche sul moto dei pianeti ed enunciata tradizionalmente così: Il raggio Sole-Pianeta spazza aree uguali in tempi uguali, vale a dire che la velocità areolare è costante: come si è visto questa non è che un'applicazione astronomica del fatto che se un corpo è soggetto ad una forza centrale il suo momento angolare è costante.
Il lavoro di una forza è, per definizione, il prodotto scalare della forza per lo spostamento.
Per calcolare il lavoro della forza di gravitazione universale relativo ad uno spostamento infinitesimo dr bisogna eseguire il prodotto scalare della forza (3.4) per lo spostamento infinitesimo (1.1)
![]()
L'espressione ottenuta è l'opposto del differenziale esatto della funzione
![]()
Riferendosi a tale funzione (detta energia potenziale gravitazionale), la (4.1) può essere scritta
![]()
Per il teorema della forze vive
![]()
Sottraendo membro a membro la (4.3) dalla (4.4)
![]()
Quindi un corpo di massa m situato nel campo gravitazionale generato dal corpo di massa M (supposto immobile nel polo O) mantiene costante nel tempo la sua energia totale E, somma della sua energia cinetica e della sua energia potenziale
![]()
Per questo motivo si dice che il campo gravitazionale è un campo conservativo.
Dalla (4.6) isolando a primo membro il quadrato della velocità si ha
![]()
Usando per v2 l'espressione (1.2.3) si ottiene
![]()
e poi
![]()
Dalla (3.5) si deduce
![]()
La (5.3) si riscrive
![]()
In definitiva
![]()
Usando ancora la (3.5)
![]()
si ha
![]()
Dividendo membro a membro la (5.6) per la (5.5) e separando le variabili
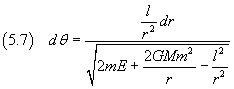
Per semplificare l'espressione del differenziale a secondo membro, conviene porre
![]()
e ancora
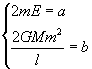
Con queste sostituzioni la (5.7) diviene
![]()
L'integrazione del differenziale a secondo membro viene facilitata scrivendo il radicando come differenza di quadrati
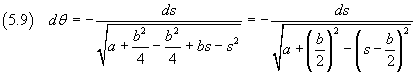
Integrando
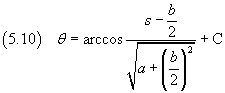
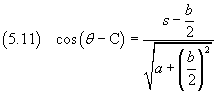
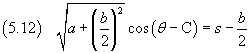
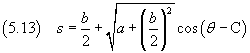
Recuperando la sostituzione per s:
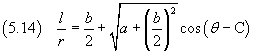
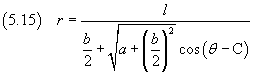
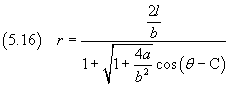
Se si impone che r sia massimo per θ=0, C= π e quindi
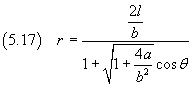
La (5.17) è l'equazione polare di una conica di parametro p ed eccentricità e dati da
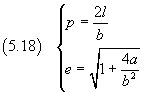
Recuperando le sostituzioni per a e b si ha
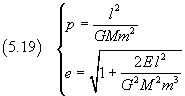
In particolare, esaminando l'espressione dell'eccentricità, si vede che
Questo risultato è più generale di quello enunciato dalla prima legge di Keplero: 'i pianeti percorrono orbite ellittiche di cui il Sole occupa un fuoco', perché prevede che i corpi celesti nel campo gravitazionale del Sole o di un altro astro percorrano anche orbite paraboliche o iperboliche.
Per semplicità ci si limita alla considerazione di orbite circolari.
Perché l'eccentricità risulti nulla e l'orbita risulti una circonferenza bisogna che
![]()
Se l'orbita è una circonferenza, la forza gravitazionale è una forza centripeta esprimibile con la (1.12)
![]()
Semplificando:
![]()
![]()
Esprimendo la velocità con la (1.10)
![]()
L'energia totale E=U+K risulta
![]()
Uguagliando le espressioni di E della (6.1) e della (6.6)
![]()
Semplificando
![]()
Esprimendo l con la (3.5)
![]()
Semplificando
![]()
Esprimendo ω con la (1.11)
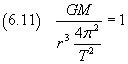
In definitiva
![]()
La (6.12) esprime la terza legge di Keplero: in un'orbita planetaria il cubo della distanza (media) del pianeta dal Sole è direttamente proporzionale al quadrato del periodo di rotazione.
Per poter calcolare la posizione di un pianeta in funzione del tempo, facendo riferimento alla figura seguente, si può procedere nel seguente modo.
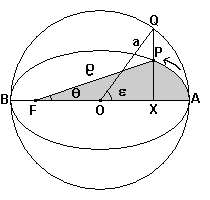
Si assume come istante iniziale il momento in cui il pianeta si trova nel punto A di massima distanza dal sole (afelio) a sua volta situato nel fuoco F dell'orbita e si indica con P la posizione del pianeta in un successivo istante t.
Si traccia la circonferenza con centro O coincidente con quello dell'orbita e raggio a uguale al semiasse maggiore a dell'orbita ellittica il cui semiasse minore è b e la cui eccentricità è e; si traccia poi la perpendicolare da P all'asse maggiore, che interseca la circonferenza nel punto Q e l'asse nel punto X.
Si indichi con ρ la distanza FP, con θ la misura dell'angolo AFP (anomalia) e con ε (anomalia eccentrica) la misura dell'angolo AOQ.
Nel sistema cartesiano di origine O e assi coincidenti con gli assi dell'ellisse la distanza FO ha misura ae e l'ascissa x è comune ai due punti P e Q.
L'equazione della circonferenza risulta
![]() quindi per l'ordinata yQ del punto Q della circonferenza si ha
quindi per l'ordinata yQ del punto Q della circonferenza si ha
![]() .
.
Nello stesso sistema di riferimento l'equazione dell'ellisse risulta
![]() e quindi per l'ordinata yP del punto P dell'ellisse si ha
e quindi per l'ordinata yP del punto P dell'ellisse si ha
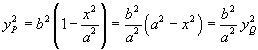 .
.
Considerando le lunghezze dei segmenti PX e QX, si ha
![]() .
.
Questo implica che:
![]()
l'area dell'ellisse è b/a dell'area del cerchio
![]()
l'area della zona di ellisse di vertici XAP è b/a di quella della zona di cerchio di vertici XAQ.
![]()
Per calcolare l'area della zona XAQ si fa la differenza tra l'area del settore circolare OAQ e quella del triangolo rettangolo OXQ. Si ottiene
![]()
e quindi
![]()
L'area di tutto il settore ellittico FAP (a fondo scuro nella figura) si ottiene aggiungendo all'area della zona XAP l'area del triangolo rettangolo FXP:
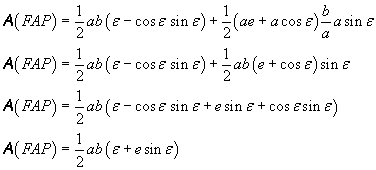
Questa è l'area 'spazzata' dal raggio vettore FP nel tempo t. Per la seconda legge di Keplero, il rapporto tra quest'area e il tempo t è costante; in particolare è uguale al rapporto tra tutta l'area dell'ellisse e l'intero periodo T di rivoluzione.
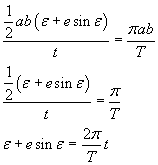
Indicando con ω la velocità angolare media
![]() si ha infine
si ha infine
![]()
Questa equazione, nota come equazione di Keplero, dati il periodo di rivoluzione T di un pianeta (o satellite) e l'eccentricità e dell'orbita, permette di ricavare (non con metodi analitici, ma con metodi di approssimazione successiva) l'anomalia eccentrica ε.
Calcolata l'anomalia eccentrica ε, si può risalire all'anomalia θ nel seguente modo
Dalla relazione tra sin θ e sin ε
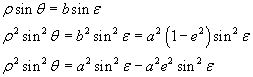
Inoltre
![]()
Sommando membro a membro le uguaglianze ottenute si ha
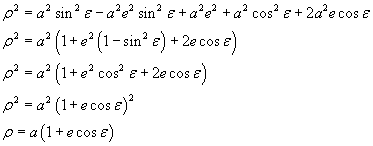
Considerando insieme
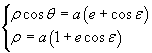
dividendo membro a membro si ha
![]()
Per le formule di bisezione
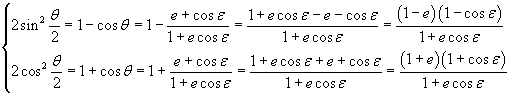
Dividendo membro a membro
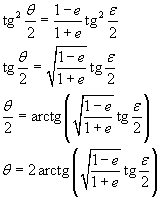
Se θ risulta negativa, aggiungere 2π.
Conoscendo θ, dall'equazione polare dell'ellisse si può ottenere il raggio vettore ρ.
ultima revisione: Giugno 2020