Se su una particella di massa m inizialmente in equilibrio nel punto O agisce una forza elastica f, cioè una forza f proporzionale allo spostamento Δr da O e di direzione opposta ad esso
![]()
l'equazione oraria del moto può essere espressa da una funzione
![]()
Una particella che si muove in questo modo è detta oscillatore armonico.
Per ricavare la (2.2) conviene scegliere un sistema di riferimento con origine nel punto O, posizione in cui la forza è nulla, e asse delle x coincidente con la direzione dello spostamento. In questo sistema la (2.1) si riduce a
![]()
Per il secondo principio della Dinamica
![]()
quindi la (2.3) diventa
![]()
Ponendo
![]()
![]()
La soluzione dell'equazione differenziale (2.7) deve essere una funzione x(t) tale che la sua derivata seconda rispetto a t sia l'opposto della funzione stessa moltiplicato per ω2. Una funzione con tali proprietà è
![]()
infatti
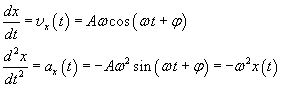
Nella (2.8) il parametro A, che rappresenta il modulo del valore massimo dello spostamento x(t), è detto ampiezza.
Il parametro φ, detto sfasamento, rappresenta l'argomento del seno all'istante t=0.
Imponendo che x(0)=0 e che v(0)=Aω, lo sfasamento risulta nullo e la (2.8) può essere scritta più semplicemente
![]()
La comprensione del senso fisico del parametro ω può essere ottenuta indicando con T il tempo che intercorre tra due massimi successivi della x(t) nella (2.9). Infatti questa funzione ha i suoi massimi quando sin ωt=1, cioè quando
![]()
allora
![]()
cioè
![]()
La grandezza T è detta periodo e può essere definito anche come durata di una oscillazione completa. Il reciproco di T, detto frequenza e indicato usualmente con ν (ni greco), rappresenta il numero di oscillazioni nell'unità di tempo:
![]()
La grandezza ω, detta pulsazione, è proporzionale alla frequenza e fornisce quindi sostanzialmente le stesse informazioni fisiche.
Usando la definizione (2.6) di ω, la (2.3) può essere scritta
![]()
Il lavoro della forza f per uno spostamento dx del suo punto di applicazione è
![]()
e la variazione di energia potenziale per uno spostamento x risulta
![]()
L'energia totale dell'oscillatore armonico risulta
![]()
L'energia dell'oscillatore armonico è costante e dipende dalla massa e dai quadrati dell'ampiezza e della pulsazione.