7. L'equazione di Schroedinger.

Se si considera l'equazione (6.5) che esprime una delle possibili funzioni d'onda associabili ad una particella vincolata a muoversi tra due barriere di potenziale

e si deriva Ψ_n due volte rispetto a x, si ottiene

Dalla (6.7) si ricava

sostituendo nella (7.1) si ha

e ancora

Introducendo il simbolo

la (7.3) viene scritta

Poiché l'uguaglianza (7.5) vale per ogni n, si può dire

L'equazione differenziale alle derivate parziali (7.6) è detta equazione di Schroedinger del sistema fisico analizzato.

L'equazione di Schroedinger è fondamentale nella descrizione del comportamento della particelle subatomiche, detta Meccanica Quantistica. Si può dire che in questa teoria ha la stessa importanza che hanno avuto i principi di Newton nella fondazione della meccanica classica ritenuta sostanzialmente valida fino alla fine dell'ottocento.

Questa equazione è stata qui dedotta in una situazione piuttosto semplice, in quanto si è analizzato un sistema unidimensionale e privo di energia potenziale. In generale per un'onda tridimensionale Ψ(x,y,z,t) e in presenza di energia potenziale U(x,y,z) essa va generalizzata così

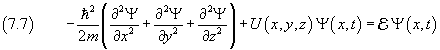
Infine, per semplificare la notazione ma anche per generalizzarla a casi più complessi, si può introdurre il simbolo H, detto operatore hamiltoniano,

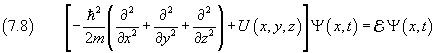
Con l'uso dell'operatore H l'equazione di Schroedinger risulta

In generale quindi per poter definire gli stati ammissibili di un sistema fisico si imposta e si cerca di risolvere l'equazione (7.9). La soluzione di tale equazione permette di determinare i valori , detti autovalori dell'operatore H, e le funzioni Ψ_n, dette autofunzioni o autostati di H.