Per sperimentare l'efficacia dell'equazione di Schroedinger in un caso molto semplice e ben analizzato, si opera ora a ritroso, mostrando come, partendo dall'equazione di Schroedinger, si deducono livelli energetici e funzioni d'onda, per una particella confinata in una scatola di potenziale di larghezza L delimitata da barriere infinite.
Bisogna risolvere l'equazione (7.9) cioè
![]()
Poiché il problema e unidimensionale e lo stato della particella non evolve nel tempo, si può sostituire alla (7.9) una sua versione semplificata:
![]()
Una funzione tale che, derivata due volte rispetto al suo argomento, produce la sua opposta è la funzione seno. Quindi si pone
![]()
Derivando la (8.2)
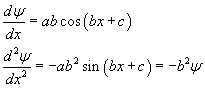
Perché la derivata seconda ottenuta coincida con la (8.1) deve essere
![]()
Inoltre la (8.2) si deve annullare per x=0 e x=L.
La prima condizione implica c=0.
La seconda dà
![]()
E quindi
![]()
Questi sono gli autovalori dell'energia.
Sostituendoli nella (8.3) si ottiene
![]()
Sostituendo b nella (8.2) si ha
![]()
Il parametro a va determinata con la condizione di normalizzazione (5.13)
![]()
![]()
dalla quale si ricava
![]()
In definitiva le autofunzioni sono
![]()