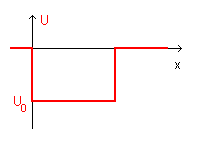
Si consideri un campo unidimensionale il cui potenziale V è ovunque nullo tranne che nell'intervallo [0;L] in cui V ha valore costante e in cui l'energia potenziale di una particella risulta negativa con valore costante U0. Un intervallo di questo genere è detto buca di potenziale (unidimensionale) di profondità U0.
Per la meccanica classica una particella situata nella buca di potenziale e con energia totale
negativa (ma beninteso
maggiore di U0) non può uscire dalla buca perché fuori di essa la sua energia cinetica
K = -0
risulterebbe negativa.
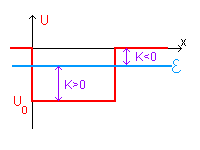
In tale campo la funzione d'onda della particella assumerà espressioni diverse nelle diverse zone del campo.
Per 0<x<L la funzione d'onda deve essere una soluzione dell'equazione (il deponente I sta per 'Interno')
Per x<0 o x>L la funzione d'onda deve essere una soluzione dell'equazione (il deponente E sta per 'Esterno')
Dato che la funzione d'onda deve essere continua e derivabile in tutto il campo, nei punti di ascissa 0 e L devono coincidere i valori delle due funzioni e delle loro derivate.
Inoltre, poiché la trattazione quantistica deve tendere asintoticamente alla meccanica classica, per x→±∞ la funzione d'onda si deve annullare.
Con un procedimento analogo a quello usato nel paragrafo 8, si assume che la soluzione della (9.1) abbia forma
e, in modo analogo, si ottiene
In questo caso, diversamente dal caso esaminato nel paragrafo 8, non sono valide le condizioni al contorno ψ(0)=0 e ψ(L)=0, perché le pareti della buca hanno altezza limitata. Quindi, per il momento, si ha
Le soluzioni della (9.2) non possono avere forma
, perché dalla derivata seconda risulta un
valore negativo per il quadrato di b.
Se si assume che la soluzione abbia forma ψ(x) = a eb x,
derivando ripetutamente rispetto a x si ha
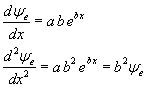
Confrontando con la (9.2) si ha
L'uguaglianza è accettabile perché, per ipotesi,
è negativa.
Fuori dalla buca quindi la funzione d'onda può avere forma
Dato che la funzione d'onda si deve annullare per x→±∞, si assume (il deponente ES sta per 'Esterno Sinistra' e il deponente ED sta per 'Esterno Destra' )
Per x=0 le due funzioni e le loro derivate devono essere uguali. Dunque
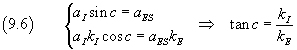
Anche per x=L le due funzioni e le loro derivate devono essere uguali. Dunque
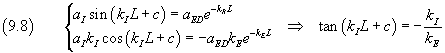
Dalle (9.6) e (9.8) si ha
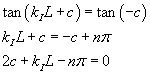
Usando le espressioni di c e kI nella (9.3) e (9.7) si ha
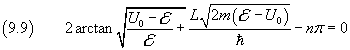
Risolvendo questa equazione rispetto a
per ogni valore di n si possono ottenere i valori dei livelli energetici all'interno della buca. Queste soluzioni
non possono essere determinate con un metodo analitico ma possono essere approssimate a piacere con un metodo numerico
scorrendo i valori di n cominciando da 1 e aumentando fintanto che le soluzioni risultano negative.
Si propone una funzione Javascript che calcoli i livelli energetici di un elettrone in una buca unidimensionale di larghezza e profondità assegnate usando il metodo di bisezione. Il codice JS è visibile usando la funzione 'mostra sorgente' del browser. La larghezza della buca va indicata in nanometri. Il potenziale all'interno della buca va indicata in modulo (viene comunque inteso come negativo) e in Volt. I livelli energetici calcolati sono espressi in elettronvolt (eV).