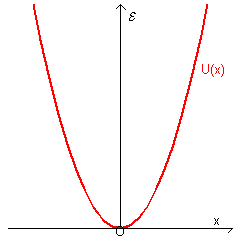
Il grafico dell'energia potenziale di un oscillatore armonico unidimensionale in funzione della distanza x dal punto di equilibrio, secondo la (2.13), è una parabola con vertice nell'origine e concavità verso l'alto.
Quindi una particella di energia totale finita
che si muove di moto armonico è contenuta in una buca di potenziale a pareti infinite; la probabilità di trovarla a
distanza infinita dal punto di equilibrio deve essere nulla.
L'equazione di Schroedinger in questo caso è
Esplicitando U(x)
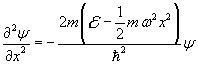
Quest'ultima equazione può essere semplificata con la sostituzione di variabile
per cui
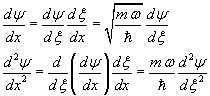
Sostituendo nel primo membro della (10.2)
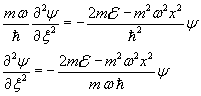
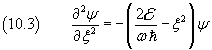
Si può semplificare ulteriormente la forma di questa equazione ponendo
quindi
La soluzione di questa equazione deve tendere a 0 per x che tende a ±∞: si può congetturare che possa essere espressa dal prodotto
dove φ(ξ) è una funzione da determinare.
Sostituendo questa espressione e la sua derivata seconda rispetto a ξ nella (10.4) si ha
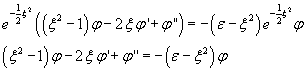
Le soluzioni della (10.7) possono essere individuate supponendo che possano essere espresse da uno sviluppo in serie
per cui
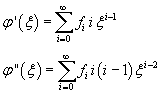
Sostituendo questi sviluppi in serie nella (10.7) si ha
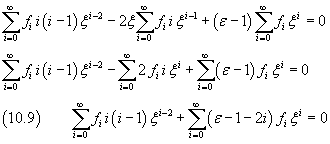
Poiché la funzione non può avere una singolarità per x=0, nella prima sommatoria si evitano gli esponenti negativi
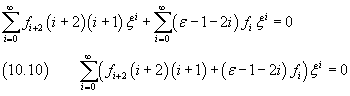
La sommatoria (10.10) è identicamente nulla se sono nulli tutti i suoi coefficienti
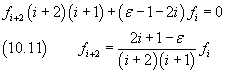
Si è così ottenuta una relazione ricorsiva tra i coefficienti dello sviluppo in serie (10.8) di φ(ξ)
Dato che φ(ξ) deve risultare finita per ogni ξ, bisogna che esita un termine n-esimo non nullo dello sviluppo tale che il temine (n+2)esimo sia nullo e quindi siano nulli tutti quelli successivi di ordine (n+4), (n+6), ecc... Dalla (10.11) si vede che ciò si verifica solo se
cioè, per la (10.4)
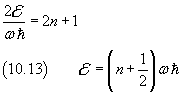
La (10.13) può essere scritta anche
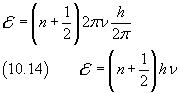
La (10.14) rappresenta un risultato fondamentale nella storia della Fisica del Novecento, perché fornisce una giustificazione teorica alla congettura di Planck e la migliora: gli oscillatori armonici, diversamente da quanto previsto dalla Meccanica Classica, non possono avere energia qualunque, ma la loro energia è quantizzata. La minima energia possibile si ha dalla (10.14) con n=0. Tutti gli altri possibili valori differiscono da questa per multipli di hν. Dunque un oscillatore armonico può emettere o assorbire energia solo scambiando con l'esterno blocchi di energia multipli di hν.