12. La funzione d'onda di una particella libera.

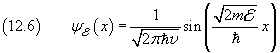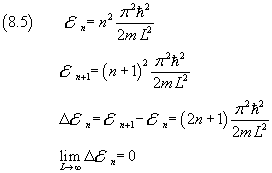
La descrizione dello stato quantomeccanico di una particella libera può essere ottenuto dai risultati conseguiti nel paragrafo 8 come caso asintotico per L (distanza tra le barriere di potenziale) tendente all'infinito.

Riprendendo la (8.5)

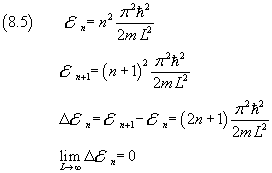
si osserva che se L→∞, cioè se la particella non è confinata in una regione limitata, cioè se è libera, la variazione di energia tra due stati contigui è infinitesimale: l'energia varia con continuità da 0 all'infinito come previsto dalla fisica classica.

La (8.5) implica inoltre che per un valore illimitato di L, se n è finito, il valore dell'energia è nullo, cosa fisicamente assurda. Perché la (8.5) converga è necessario che al tendere di L all'infinito, n tenda all'infinito nello stesso modo e quindi sia proporzionale a L. Insomma, n non può essere un numero naturale.

Si può tuttavia continuare ad imporre che nella funzione d'onda c sia nullo. Questo equivale ad assumere come origine delle posizioni quella di un punto in cui la funzione d'onda si annulla. Dato che tale posizione non ha un estremo superiore, la x può variare da -∞ a + ∞ e apparire positiva per un'onda progressiva, negativa per un'onda regressiva.

Rimane valida anche la (8.3), cioè

per cui, data l'energia di una particella, la funzione d'onda progressiva corrispondente deve avere forma

.

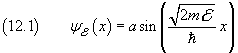Ricordando la relazione tra energia cinetica e quantità di moto p si ha, un po' più semplicemente,

L'ampiezza dell'onda è ora indicata con α perché la sua determinazione dipende dalla procedura di normalizzazione adottata.

Il valore del parametro α va determinato dalla condizione di normalizzazione che però non può essere data uguagliando a 1 l'integrale del quadrato della (11.2) da -∞ a +∞ in quanto questo integrale, che è sostanzialmente una somma di infinite quantità tutte positive, diverge. Dato che la ψ_p varia con continuità al variare di p, dato il valore p₀, la ψ_p corrispondente a p₀ è data dal valor medio integrale <ψ_p> nell'intervallo da p₀ a p₀+Δp

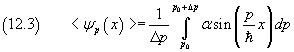
Integrando si ottiene

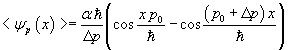
Considerando onda progressiva e onda regressiva, la condizione di normalizzazione risulta

Integrando si ottiene

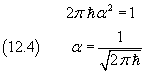
Quindi la (12.2) può essere più compiutamente scritta come

Osservando che

sostituendo il differenziale nella (11.3) si ha

Si ottiene

.

In definitiva la funzione d'onda di una particella libera di energia risulta