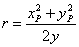La determinazione della carica specifica dell'elettrone è una delle misure fondamentali della fisica: conoscendo tale rapporto e il valore di una delle due grandezze, infatti, si può risalire facilmente a quella sconosciuta.
L'esperienza delle bobine di Helmholtz permette proprio di rilevare il valore di questo rapporto, sfruttando le relazioni fondamentali dell'elettromagnetismo.
Un filo conduttore percorso da corrente (i) genera un campo magnetico (B): per calcolare l'intensità di tale campo in un punto P situato nello spazio intorno al filo si possono sommare gli effetti prodotti da elementi infinitesimali di filo
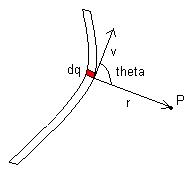
Considerando l'immagine si può ipotizzare che un contributo infinitesimo di campo dB sia proporzionale ad un quantità di carica dq, alla sua velocità v e al seno dell'angolo θ formato dalla congiungente il punto P e un segmento dl di filo in cui si muove la carica; inoltre, per analogia con il campo elettrico dB sarà inversamente proporzionale al quadrato della distanza r, per cui:
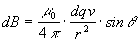
e dove μ0 è una costante detta permeabilità magnetica del vuoto, il cui valore è:
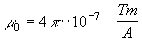
L'equazione prende il nome di legge di Laplace, la cui forma vettoriale risulta
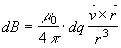
Inoltre ricordando che
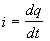
e che
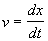
L'equazione può così essere scritta
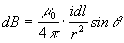
CAMPO MAGNETICO GENERATO DA UNA SPIRA PERCORSA DA CORRENTE

L'immagine mostra una spira circolare percorsa da corrente; per calcolare il campo magnetico si utilizza la legge di Laplace: come si può notare dalla figura la simmetria della spira è tale da annullare le componenti di dB parallele all'asse x, pertanto si considerano esclusivamente le componenti sull'asse y il cui modulo risulta
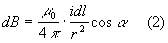
Il cosα può essere scritto nel modo seguente
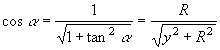
Il campo magnetico totale si ottiene integrando la (2) per tutta la lughezza della spira, pertanto, portando fuori dall'integrale le costanti, si ottiene
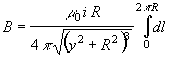
Sviluppando e semplificando si ottiene perciò
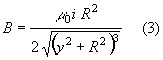
LE BOBINE DI HELMHOLTZ E LA DETERMINAZIONE DELLA CARICA SPECIFICA DELL'ELETTRONE
L'esperienza delle bobine di Helmholtz si basa sulla formazione di un campo magnetico mediante l'utilizzo di spire in un punto posto ad una distanza pari alla metà del raggio della spira: in tal caso, dalla (3) si ricava che l'intensità di B nel punto risulta

essendo necessario ai fini dell'esperimento un campo di intensità elevata, si ricorre all'uso di bobine ovvero di insiemi di n spire in modo da ottenere un campo n-volte maggiore. Più precisamente si usano due bobine uguali poste, tra loro, a distanza pari al loro raggio per far sì che gli effetti siano raddoppiati, infatti, l'intensità di B nella zona in mezzo alle due bobine risulta essere
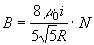
La determinazione della carica specifica dell'elettrone avviene facendo passare in mezzo alle due bobine un fascio di elettroni a velocità v; ciò si può ottenere ponendo un tubo a raggi catodici in mezzo alle bobine.
In corrispondenza del catodo gli elettroni hanno energia potenziale U pari a
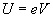
Giunti all'anodo, gli elettroni avranno solo energia cinetica che, per il principio di conservazione dell'energia risulta
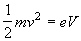
Per cui
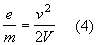
Il fascio di elettroni, inoltre, interagendo con il campo magnetico viene sottoposto alla forza di Lorentz
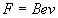
che risulta perpendicolare alla velocità e funge da forza centripeta facendo entrare gli elettroni in moto circolare di cui, nel caso dell'eperimento viene evidenziato solo un arco di circonferenza; dalle relazioni del moto circolare risulta dunque
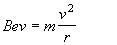
Pertanto il rapporto carica massa risulta
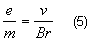
Eguagliando la (4) e la(5) si ricava che la velocità è pari a
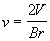
Sostituendo nella (5) si può concludere che il rapporto cercato risulta essere
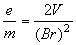
Per ottenere informazioni relative al raggio della circonferenza percorsa si può porre dietro al fascio di elettroni un supporto su cui è rappresentato un piano cartesiano quadrettato in cm in modo che l'origine dell'arco di circonferenza venga a coincidere con l'origine degli assi. L'equazione di circonferenza di centro C(0;R) e raggio r sarà:
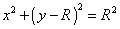
Individuato nel piano un punto P in cui passi l'arco della circonferenza, pochè le coordinate del punto devono soddisfare l'equazione della curva, il raggio risulta essere