GIACOMO CALANCHI - CLASSE 5N - A.S. 2006/2007

I solidi semiconduttori
Risultati degli esperimenti di interazione tra fotoni ed elettroni

PROGETTO LAUREE SCIENTIFICHE

Università di Bologna - Facoltà di Fisica

1. Introduzione allo studio dei solidi semiconduttori

1.1 Elettroni e atomi

Per lo studio e l’analisi dei fenomeni microscopici che avvengono all’interno dei semiconduttori occorre conoscere il comportamento delle particelle a livello atomico.

Gli elementi protagonisti sono gli elettroni: i processi e le proprietà che li caratterizzano sono responsabili di gran parte dei fenomeni molecolari.

L’aspetto più rilevante per lo studio dei semiconduttori è l’applicazione della meccanica quantistica alla descrizione degli elettroni (e quindi dei loro stati) all’interno di un solido. Questa teoria fornisce unicamente indicazioni statistiche sulla possibilità che una particella occupi o meno una regione di spazio. Uno dei fondamenti della meccanica quantistica infatti è il principio di indeterminazione di Heisenberg che prevede l’impossibilità di determinare velocità e posizione di un elettrone congiuntamente e dunque di descriverne il moto in maniera deterministica. All’orbita elettronica viene sostituita la funzione orbitale elettronico. Questa descrive la densità della nube elettronica, cioè la distribuzione di probabilità dell’elettrone attorno al nucleo.

Inoltre, l’energia di una elettrone che si muove all’interno di un campo di forze attrattive non può assumere qualsiasi valore ma solo alcuni valori detti livelli energetici. La funzione dell’energia non è continua bensì discreta, quantizzata. Il livello più basso di energia (dove l’elettrone è più vicino al nucleo) è definito stato fondamentale, mentre gli altri (dove l’elettrone ha maggiore energia) stati eccitati o livelli e sono instabili, in quanto l’elettrone, cedendo energia sotto forma di onde elettromagnetiche, tende ad occupare livelli con energia inferiore. Lo stato fondamentale è stabile poiché è il valore base sotto il quale non si può scendere (infatti i quanti non sono frazionabili).

L’emissione e l’assorbimento di energia da parte di un atomo, quindi lo spostamento di un elettrone da un livello ad un altro, sono definiti dall’equazione

dove h è la costante di Planck ( ) e ν è la frequenza.

A seconda del numero di elettroni e del numero di livelli presenti in un atomo si modificano le proprietà chimico/fisiche dello stesso.

1. Divisione dei livelli energetici

Gli elettroni più interni, più vicini al nucleo, sono troppo vincolati ad esso per interagire “con l’esterno”. La struttura degli elettroni interni e del nucleo non è modificata dalla ricombinazione della nube elettronica di un atomo. Il nucleo e gli elettroni molto prossimi ad esso vengono definiti nocciolo ionico. Gli elettroni più esterni sono la causa di tutti i processi caratteristici dell’atomo stesso (legame chimico, interazione fotoelettrica, spettri di assorbimento/emissione). Sono chiamati elettroni di valenza. Questo valore definisce la capacità di un elemento di a combinarsi con uno o più atomi (numero di legami).

1.2 Legami atomici

In natura è molto difficile trovare elementi “puri” al 100%, poiché gli atomi tendono a completarsi vicendevolmente interagendo a livello elettronico. Come si è detto gli elettroni di valenza sono i responsabili dei legami interatomici e, in generale, gli atomi tendono a completare quest’area raggiungendo la situazione di equilibrio, data da otto elettroni (regola dell’ottetto). Infatti, ad un minor numero di elettroni di valenza corrisponde una maggior tendenza dell’atomo ad integrare la mancanza attraverso legami con altri e viceversa.

Quando due atomi si avvicinano tra loro, le cariche in gioco danno origine a forze e le nubi elettroniche si distorcono modificando i livelli energetici. Legandosi, il sistema formato dai due atomi arriva ad uno stato, più stabile, di minore energia.

Vi sono varie tipologie di legame: covalente, ionico e metallico più altri tipi di interazione debole. Per lo studio dei semiconduttori è necessario conoscere le proprietà del legame covalente che si instaura tra due atomi con elettronegatività (capacità degli atomi di attrarre elettroni) uguale o simile. Questi possono legarsi mettendo in comune una coppia di elettroni, ciascuna delle quali determina un legame covalente. Gli orbitali degli elettroni di valenza si perturbano e danno origine ad una nube elettronica che avvolge la congiungente interatomica, descritta dalla funzione orbitale molecolare. Il numero di legami covalenti che un elemento può stabilire è pari al numero di valenza dello stesso.

2. - Fasi di formazione del legame covalente

1.3 Solidi e cristalli, imperfezioni e impurezze

Un legame rigido, definito e regolato da un’energia di notevole entità, tra milioni e milioni di atomi (occorre sempre fare i conti con il numero di Avogadro ) origina un solido, il quale ha, al suo interno, una disposizione definita delle particelle che lo compongono. Esistono due possibili disposizioni: disordinata che forma solidi amorfi (es. vetro); ordinata, regolare che forma solidi cristallini (o cristalli). I solidi cristallini prevedono una disposizione geometrica organizzata e costante (entro limiti che verranno descritti) degli atomi, queste posizioni rappresentano il reticolo cristallino.

Il reticolo cristallino è formato dalla ripetizione di migliaia di celle elementari che costituiscono l’unità base del cristallo e può essere ottenuto dalla sovrapposizione di più celle unitarie.

In natura un reticolo cristallino perfettamente organizzato è un caso limite, impossibile da raggiungere. Infatti ogni cristallo contiene imperfezioni strutturali e/o molecolari.

Morfologicamente le imperfezioni sono divise in:

• puntiformi: coinvolgono uno o pochi atomi, sono sempre presenti nei solidi
• lineari: lungo una linea che attraversa parti del solido, gli atomi non occupano posizioni reticolari normali
• planari: un’ampia area separa due zone con orientazioni reticolari distinte

Le imperfezioni modificano, a seconda della loro entità, alcune proprietà del solido.

Oltre alle imperfezioni strutturali concorrono a modificare particolari parametri (soprattutto la conducibilità) del solido anche le impurezze, cioè atomi estranei al cristallo standard che entrano nel reticolo in posizioni vicariali, in quantità più o meno consistenti. In ogni caso un solido “purissimo” contiene almeno 10⁶ impurezze per metro cubo.

1.4 Struttura elettronica e bande

Durante la formazione di solidi cristallini gli orbitali atomici si fondono componendo orbitali cristallini estesi a tutto il volume occupato dal medesimo. Gli elettroni di valenza non risultano più legati ad un unico atomo ma sono in grado di spostarsi all’interno del volume, sono delocalizzati. A questi non corrispondono più livelli discreti di energia ma moltissimi valori vicinissimi tra loro. Questi intervalli sono definiti bande di energia, poiché al loro interno i livelli energetici sono praticamente continui. La banda energetica più esterna è la banda di valenza.

Queste bande possono essere separate da intervalli che non sono occupati da nessun elettrone: sono detti intervalli proibiti o gap energetici. I gap hanno un’importanza notevole nello studio dei conduttori, dei semiconduttori e degli isolanti e caratterizzano soprattutto la conducibilità dei solidi. Infatti quest’ultimo parametro dipende da quanto gli elettroni “sono lasciati liberi” di scorrere lungo il volume del solido, se sottoposti ad una differenza di potenziale, cioè di acquisire energia cinetica da un campo elettrico. Per questo è opportuno definire il concetto di banda di conduzione, ovvero l’insieme di quei livelli energetici (molto vicini) che, assunti dagli elettroni, permettono loro di acquisire una determinata velocità all’interno del reticolo, se sottoposti ad una differenza di potenziale. Secondo queste proprietà sono definite tre classi di solidi:

• nei metalli, gli elettroni di valenza sono liberi di muoversi poiché sono poco legati agli atomi originari. Una volta formato il solido, gli elettroni non sono legati a singoli atomi bensì all’intero reticolo, formando una sorta di “gas elettronico” (modello di Drude, velocità di deriva). La banda di valenza e la banda di conduzione, in un metallo, sono, per buona parte, coincidenti, dunque hanno un’ottima conducibilità.
• negli isolanti, gli elettroni di valenza formano stretti e rigidi legami tra gli atomi circostanti e quindi non possono essere spostati da un campo elettrico. Questo significa, in termini di bande energetiche, che esiste un ampio energy gap tra la banda di valenza e quella di conduzione; nella banda di valenza tutti i livelli sono occupati, in quella di conduzione sono tutti liberi.
• il caso dei semiconduttori sarà esaminato in seguito.

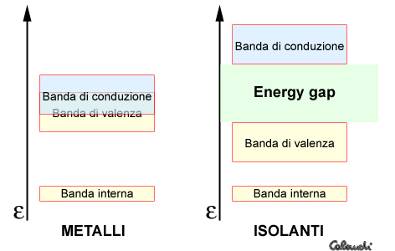
3. - Bande nei metalli e negli isolanti

2. Caratteristiche e proprietà dei semiconduttori

2.1 Proprietà generali dei semiconduttori

I semiconduttori sono elementi (es. silicio, germanio e gallio) o composti (es. arseniuro di gallio, arseniuro di gallio e alluminio, antimoniuro di indio, fosfuro di indio...) che presentano particolari caratteristiche elettriche ed elettroniche:

• hanno una resistività intermedia tra isolanti e conduttori ( ). A basse temperature sono buoni isolanti viceversa ad alte temperature conducono.
• Le proprietà elettriche sono molto sensibili alla conformazione reticolare del cristallo (impurezze e imperfezioni).
• Sono buoni fotoconduttori.

2.2 Livelli e bande nei semiconduttori

La spiegazione alla variazione sostanziale di resistività, alla dipendenza delle proprietà elettriche dalla conformazione reticolare del cristallo e la fotoconducibilità sono da ricercarsi nella struttura delle bande nei solidi cristallini semiconduttori. Queste infatti non differiscono qualitativamente dagli isolanti (dove è presente un ampio gap energetico tra banda di conduzione e banda di valenza) ma quantitativamente. Nei semiconduttori questi valori proibiti di energia hanno un intervallo sensibilmente inferiore che può essere superato. Fornendo al reticolo una quantità di energia non elevata, è possibile sciogliere legami elettronici e svincolare gli elettroni dalle loro posizioni standard promuovendoli nell’area di conduzione.

4. - Bande nei semiconduttori

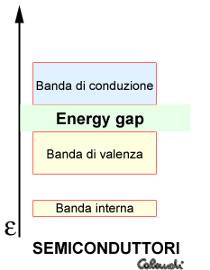
2.3 Elettroni, lacune e conducibilità nei semiconduttori

Quando un elettrone è “promosso” da banda di valenza a banda di conduzione lascia un livello “vuoto”. A livello di legame, viene rotto il rapporto con l’atomo al quale era vincolato e si crea un buco nel reticolo cristallino.

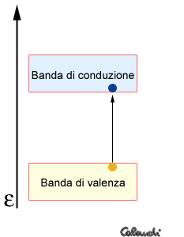
5. - Coppia elettrone/lacuna

Questa mancanza è definita lacuna ed è un fenomeno frequente nei cristalli semiconduttori a temperatura ambiente. La peculiarità delle lacune è che si comportano, all’interno di un solido sottoposto ad una differenza di potenziale, proprio come gli elettroni: si muovono. Avendo formalmente carica opposta agli elettroni si spostano in direzione contraria ad essi. Ciò è provocato dallo spostamento di elettroni di valenza degli atomi circostanti che si muovono e vanno ad occupare il posto lasciato vuoto, generando, a loro volta, altre lacune. Questo significa che, applicando una tensione ai capi di un cristallo semiconduttore a temperatura ambiente, la corrente coinvolgerà sia elettroni di conduzione sia lacune. Da ciò ne deriva che la conducibilità, in un semiconduttore, dipende sia dalle cariche negative (elettroni) sia dalle cariche positive (lacune).

È possibile ricavare, facendo riferimento al modello di Drude, le espressioni della conducibilità.

Essendo il reciproco della resistività si ottiene:

Sostituendo la formula della resistività si ottiene:

dove m_e è la massa dell’elettrone, n_e è il numero di elettroni, e è la carica dell’elettrone e τè il tempo libero medio (tempo medio tra le collisioni degli elettroni con gli atomi eccitati del reticolo cristallino).

Da questa relazione è possibile isolare la variabile mobilità:

Ricavata questa formula è possibile definire quella della conducibilità in un semiconduttore:

2.4 Semiconduttori intrinseci ed estrinseci

Come descritto nel paragrafo 1.3, ogni cristallo contiene impurezze. Anche i solidi definiti “puri” hanno, nel reticolo cristallino, atomi non dello stesso elemento chimico. Ciò che rende i semiconduttori così modificabili per le varie esigenze tecnologiche, è la capacità che hanno di variare la conducibilità in funzione della densità e del tipo di impurezze.

In un cristallo semiconduttore puro, che contiene al suo interno una densità trascurabile di impurezze, la conducibilità è determinata dalla promozione di elettroni da banda di valenza a banda di conduzione, per eccitazione termica (par. 2.5) e, quindi, dalla creazione di coppie lacuna-elettrone. Un cristallo di questo tipo, a temperatura ambiente, ha scarsa conducibilità, determinata dal basso numero di coppie elettrone-lacuna e il rapporto elettroni/lacune è uguale a 1.

In un cristallo semiconduttore, nel quale siano state inserite artificialmente impurezze (drogato), la conducibilità è determinata, per buona parte, dal tipo e dalla concentrazione delle medesime. Esistono due tipi di impurezze:

• donori: sono atomi che cedono facilmente elettroni di valenza alla banda di conduzione del cristallo.
• accettori: sono atomi che mancano di un elettrone di valenza. Ciò crea una lacuna attorno all’atomo accettore.

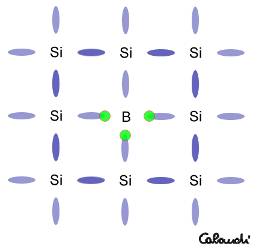
6. - Impurezza donore e impurezza accettore - Un atomo di silicio è sostituito da uno di fosforo pentavalente (sinistra) oppure da uno di boro trivalente (destra)

Variando il tipo di impurezza è possibile determinare quali saranno, all’interno del semiconduttore, i portatori maggioritari, cioè quale tipo di carica prevarrà sull’altra.

Sono definiti semiconduttori di tipo n quelli con impurezze donori, all’interno dei quali i portatori maggioritari sono elettroni della banda di conduzione; sono definiti semiconduttori di tipo p quelli con impurezze accettori, dove i portatori maggioritari sono lacune della banda di valenza.

I semiconduttori presentano due tipi di comportamento, in funzione delle impurezze interne:

• regime estrinseco: i portatori maggioritari sono determinati dalle impurezze.
• regime intrinseco: i portatori maggioritari sono determinati dalle proprietà caratteristiche dei semiconduttori (par. 2.5) e il ruolo delle impurezze è trascurabile ai fini della conducibilità.

2.5 Importanza della temperatura e delle onde elettromagnetiche

Allo zero assoluto (0° K) un semiconduttore presenta conducibilità uguale a zero. A temperatura ambiente questo parametro è maggiore. Ciò è dovuto all’energia termica irraggiata, dall’esterno, nel cristallo semiconduttore. Infatti, alla temperatura asintotica di 0° K, il reticolo cristallino è immobile e gli elettroni di valenza sono saldamente vincolati, da legami covalenti, ai propri atomi. Con l’aumentare della temperatura viene fornita energia termica al solido, gli atomi aumentano la loro eccitazione e ciò provoca la rottura di alcuni legami elettronici e la produzione di coppie elettrone-lacuna. A livello di bande, questo significa dare all’elettrone un’energia superiore a quella del gap energetico tra banda di valenza e banda di conduzione.

Formalmente la concentrazione di elettroni e di rispettive lacune è descritta dalla funzione:

dove K_B è la costante di Boltzmann ( ), E_G è l’energy gap e T è la temperatura.

Un fenomeno con effetti simili deriva dalle peculiari proprietà ottiche dei semiconduttori. Anche in questo caso l’interpretazione si trova nella teoria delle bande. Infatti, quando si illumina un cristallo semiconduttore, lo si investe di una certa quantità di energia determinata dall’equazione

Si presentano due casi:

• , i fotoni spariscono cedendo l’energia agli elettroni di valenza che vengono promossi in banda di conduzione, lasciando nella banda di valenza una lacuna. L’energia dei fotoni è quindi assorbita dal cristallo e non viene trasmessa al di fuori di esso. Per questo intervallo di frequenze il cristallo non risulterà oltrepassabile dalle radiazioni elettromagnetiche. Questo fenomeno è definito fotoconduttività.

• , i fotoni non danno luogo a nessuna reazione da parte del cristallo. La radiazione elettromagnetica, in questo intervallo di frequenza, potrà oltrepassare il solido semiconduttore.

  

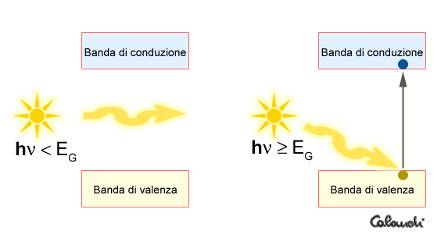
  7. - Schema della produzione di coppie elettroni/lacune per effetto fotoelettrico interno

3. Esperimenti sull’energy gap dei semiconduttori

3.1 Analisi delle proprietà elettriche di metalli e semiconduttori

Scopo dell’esperimento è l’osservazione del comportamento della resistività in metalli e semiconduttori entro un certo range di temperature e l’analisi delle differenze tra questi.

3.1.1 Descrizione dell’apparato sperimentale

La strumentazione utilizzata è composta da:

• dewar, contenitore in grado di mantenere un livello di isolamento termico elevato. È realizzato interponendo, tra la camera interna e l’ambiente esterno, uno o più strati sotto vuoto (il vuoto non conduce calore per conduzione o convezione, ma solo per irraggiamento) ed è isolato dalle principali radiazioni esterne grazie ad uno strato metallico riflettente. Le pareti interne sono sottili così da minimizzare gli scambi di calore.
• cestello di ottone, collegato alla sommità del dewar ed inserito nella sua camera, contenente i campioni da analizzare (rame, nichel e germanio), un termometro a diodo ed un riscaldatore per effetto Joule. Nella parte più bassa del cestello è saldata una barra metallica, detta dito freddo, a contatto con il liquido refrigerante.
• azoto liquido, usato come refrigerante per portare i campioni a temperature molto basse, nell’ordine di 130°/140° K.
• unità elettronica di controllo, utilizzata per il pilotaggio del riscaldatore, la conversione dei segnali elettrici (tensione, corrente), provenienti dal termometro a diodo e dai campioni, in segnali analogici e il monitoraggio in tempo reale della temperatura del termometro a diodo.
• interfaccia per pc, collegata all’unità di controllo, serve a trasmettere, in formato digitale, i dati provenienti dall’unità di controllo.

8. - Strumentazione

3.1.2 Esecuzione dell’esperimento

È stato versato, all’interno del dewar, azoto liquido a sufficienza per immergere il dito freddo. Dopo aver chiuso la camera interna con il coperchio alla sommità, è stato osservato il calo di temperatura tramite il display situato sull’unità elettronica di controllo. Raggiunta una temperatura stabile di 135°K (al di sotto della quale non è stato possibile andare) è stata avviata la registrazione, secondo per secondo, delle resistenze dei vari campioni e della temperatura ed è stato acceso il riscaldatore. La registrazione si è conclusa a 411°K.

3.1.3 Analisi dei dati e studio dei fenomeni

Di seguito sono riportati i grafici della variazione di temperatura in funzione del tempo e della variazione di resistenza dei campioni in funzione della temperatura del sistema.

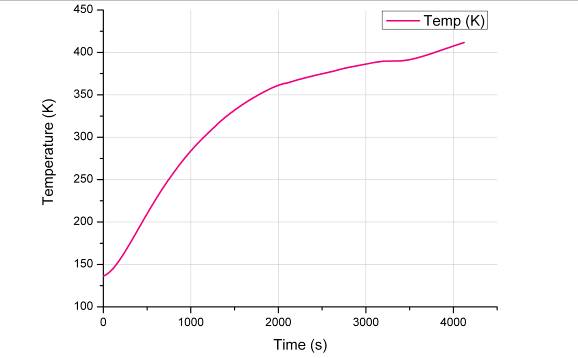
1 - Variazione della temperatura in funzione del tempo

Come si intuisce dall’andamento della curva, il cestello di ottone non varia costantemente la sua temperatura (infatti la curva non è monotona) ma presenta degli intervalli in cui essa non cresce. In questi lassi di tempo la massa dell’ottone è più lenta ad acquisire calore dal riscaldatore.

Il range di temperature registrato varia da 136,63°K a 411,6°K.

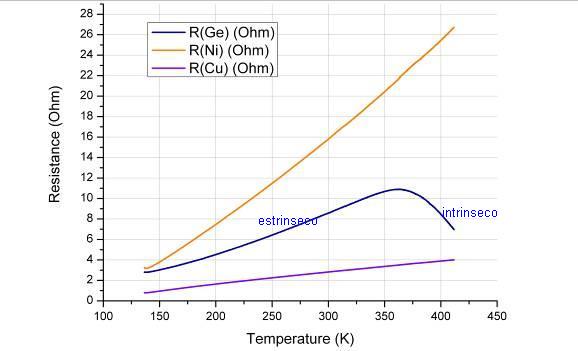
2 - Variazione della resistenza dei campioni in funzione della temperatura

Già dall’andamento delle tre curve si nota la differenza tra metalli e semiconduttore. I metalli presentano curve monotone, approssimabili a rette. In particolare, il rame presenta un comportamento che verifica perfettamente le leggi di Ohm. Il campione di germanio reagisce in due modi differenti alla temperatura. In un primo intervallo termico (da 136°K a circa 360°K) il campione si comporta, con buona approssimazione, come un conduttore ohmico. Da 360°K circa, il campione assume un comportamento opposto, diminuendo drasticamente la resistenza all’aumentare della temperatura. Nel primo intervallo termico il germanio è in regime estrinseco, i portatori maggioritari sono determinati dalle impurezze, di tipo n, all’interno del cristallo, la resistenza aumenta con la temperatura poiché diminuisce la mobilità. Nel secondo intervallo termico il campione è in regime intrinseco, i portatori maggioritari sono determinati dalla relazione che lega elettroni/lacune alla temperatura, il ruolo delle impurezze è trascurabile.

Per l’analisi dell’energy gap, allo zero assoluto, occorre analizzare appunto quest’ultima zona del grafico.

Il grafico di , nell’intervallo termico a regime estrinseco, rappresenta una curva che, con buona approssimazione, è una retta . Il coefficiente angolare è dove Eg(0) è l’energy gap a 0°K e K_B è la costante di Boltzmann ( ).

[Questo metodo è utilizzato “così com’è”, senza fornirne una motivazione matematica che sconfinerebbe in analisi statistiche al di fuori dei programmi ministeriali della scuola secondaria.]

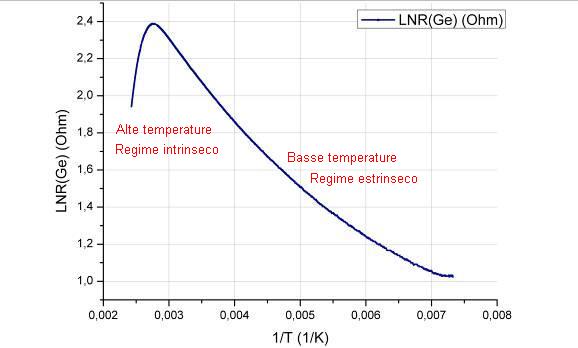
3 - LNR(Ge) in funzione di 1/T

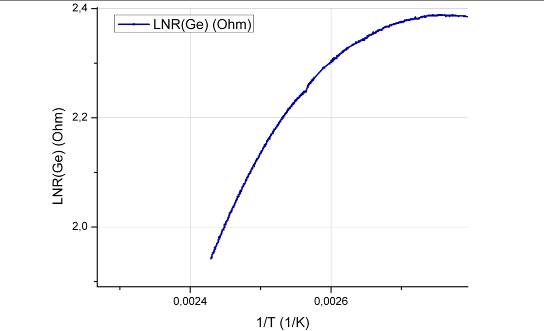
4 - Particolare del grafico LNR(Ge) in funzione di 1/T della zona intrinseca

Per determinare la suddetta retta occorre cercare il coefficiente della retta di regressione lineare (che approssima l’andamento della curva ). Utilizzando questa funzione con un programma di elaborazione dei dati, si ottiene il valore .

Sostituendo alla formula il valore a si ottiene

convertendo il risultato in eV si ottiene

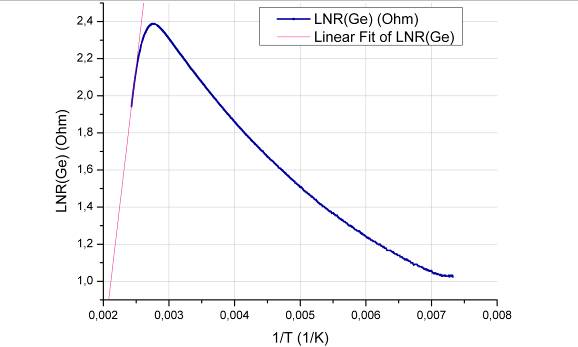
5 - Regressione lineare del grafico LNR(Ge) in funzione di 1/T

Confrontando questo risultato con il valore dell’energy gap standard ( ) si nota un’inesattezza consistente. Ciò è dovuto all’errore di misurazione del termometro a diodo che, influenzato dal rumore esterno, ha inviato dati imprecisi per molti valori. Come risulta dall’ingrandimento del grafico precedente, la curva non è ben definita ma presenta punti “incoerenti”.

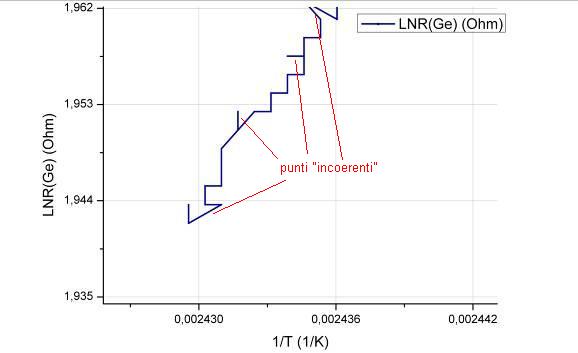
6 - Zoom della zona ad alta temperatura

3.2 Analisi delle proprietà ottiche dei semiconduttori

Scopo dell’esperimento è l’analisi della variazione di conducibilità nei semiconduttori, stimolati da onde elettromagnetiche di diversa lunghezza d’onda e, di conseguenza, diversa energia e l’interpretazione dell’effetto fotoelettrico interno per la ricerca dell’energy gap.

3.2.1 Descrizione dell’apparato sperimentale

La strumentazione utilizzata è formata da diverse apparecchiature che svolgono, nell’economia dell’esperimento, funzioni diverse. Possono essere divise in:

• emissione/diffrazione della luce:

  • lampada con spettro di emissione compreso tra il visibile e il vicino infrarosso.
  • reticolo cristallino con proprietà di diffrazione a riflessione note, posizionato su una base rotante, controllata da un sistema elettronico, sulla quale sono riportati i gradi della normale al reticolo rispetto la direzione del fascio luminoso. Questo reticolo ha proprietà tali da restituire, se colpito da un fascio di luce bianca (quindi contenente tutte le lunghezze d’onda dello spettro visibile), un fascio di luce monocromatica (con lunghezza d’onda definita) in funzione dell’angolo descritto dalla normale al piano reticolare rispetto alla direzione del fascio luminoso proveniente dalla lampada.
  • prima lente, inserita tra la lampada e il reticolo, realizzata in modo tale da concentrare il fascio di luce lungo tutta la superficie del cristallo di diffrazione.
  • seconda lente, inserita tra cristallo di rifrazione e campione semiconduttore per concentrare il fascio di luce sul campione.

• produzione/rilevazione dei segnali elettrici:

  • generatore di corrente collegato al campione da analizzare.
  • misuratore voltamperometrico.
  • sensore piroelettrico, un dispositivo sensibile alle variazioni di illuminamento. In particolare questo elemento produce una corrente alternata quando è illuminato da luce intermittente (fondamentale per la riduzione del rumore di fondo).
  • riduzione dei disturbi ambientali, amplificazione dei segnali necessari:
  • chopper, disco forato in modo regolare e costante posto davanti alla sorgente luminosa. Ruotando, spinto da un motore elettrico, restituisce un impulso luminoso approssimabile ad un’onda quadra (foro=luce, parete=buio).
  • amplificatore lock-in, amplifica solo i segnali “puri” ricavati dalla frequenza di rotazione del chopper. Opera combinando i segnali del chopper, del piroelettrico (che ha una frequenza uguale a quella del chopper) e del campione. Analizzando la frequenza di rotazione del disco amplifica i segnali buoni (quando dal chopper esce luce) e riduce i segnali spuri. Poiché le correnti in questione sono nell’ordine dei mV, anche quando il campione e il piroelettrico non ricevono luce, all’amplificatore giungono correnti generate dal rumore esterno e dalle interferenze.
  • interfaccia pc, converte i segnali elettrici in segnali digitali.

Di seguito è riportato lo schema dei collegamenti:

3.2.2 Esecuzione dell’esperimento

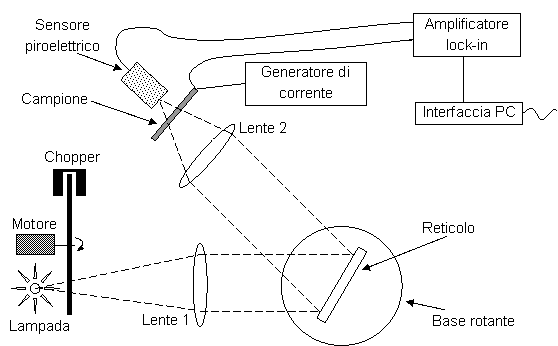
È stata fatta ruotare la base rotante del reticolo di diffrazione fino a raggiungere un angolo (tra la normale allo stesso e la direzione del fascio luminoso) di 60° ( ).

È stato posizionato il campione semiconduttore tra la lente 2 e il sensore piroelettrico e, dopo aver configurato il software di registrazione dati in funzione dell’angolo descritto dalla base rotante del reticolo di diffrazione, è stato avviato l’intero apparato strumentale (motore del chopper, lampada, amplificatore lock-in e base rotante del reticolo di diffrazione). La base rotante ha velocità angolare .

Il software di raccolta dati fornisce la registrazione di quattro valori in tempo reale:

• tempo: misurato in secondi con intervalli di rilevazione di 0,1s.
• potenziali: relativi al sensore piroelettrico e al campione semiconduttore, misurati in volt.
• angolo di rotazione della base rotante: misurato in gradi e convertito in radianti.

La registrazione dei valori è stata effettuata facendo girare il cristallo di diffrazione di 120° (la normale al reticolo ha descritto angoli da -60° a +60° rispetto la direzione di propagazione del fascio luminoso) in un tempo di 100 secondi.

3.2.3 Analisi dei dati e studio dei fenomeni

Il grafico dei potenziali in funzione della lunghezza d’onda (dipendente dall’angolo descritto dal reticolo di diffrazione) mostra gli andamenti delle tensioni.

È interessante notare che:

• il reticolo di diffrazione non ha un comportamento costante per angoli positivi o angoli negativi. Infatti, data la sua conformazione reticolare, diffrange la luce in maniera diversa, restituendola più o meno intensa (si nota chiaramente dal potenziale del piroelettrico).
• la lunghezza d’onda per l’angolo , ovviamente, non è (ciò deriva dall’applicazione della formula descritta dopo) ma rappresenta uno spettro di lunghezze d’onda composito (essendo luce bianca ha tutte le lunghezze d’onda dello spettro visibile). È evidente che, in questa circostanza, le energie non sono quantificabili considerando un’unica lunghezza d’onda. Si nota nel grafico un picco vistoso che ne è la prova.
• le lunghezze d’onda, unità di misura dell’asse delle ascisse, sono per metà negative. Ciò rappresenta le lunghezze d’onda dei fasci monocromatici generati dall’angolo di rotazione negativo ed è convenzionale in quanto le lunghezze d’onda sono sempre positive.

Per un’analisi più approfondita riguardo le energie occorre determinare il rapporto tra angolo descritto dal cristallo di diffrazione e lunghezza d’onda del fascio luminoso monocromatico emesso dallo stesso.

Le specifiche della strumentazione offrono la formula per determinare la lunghezza d’onda della luce monocromatica (misurata in nm) in funzione dell’angolo descritto dalla normale al reticolo

dove i coefficienti sono dati dal costruttore e sinθ è il seno dell’angolo descritto, espresso in radianti.

L’energia del fascio luminoso monocromatico sarà

ricordando che

Stabilito il rapporto tra angolo ed energia si può passare all’analisi dei grafici, per determinare il valore dell’energy gap.

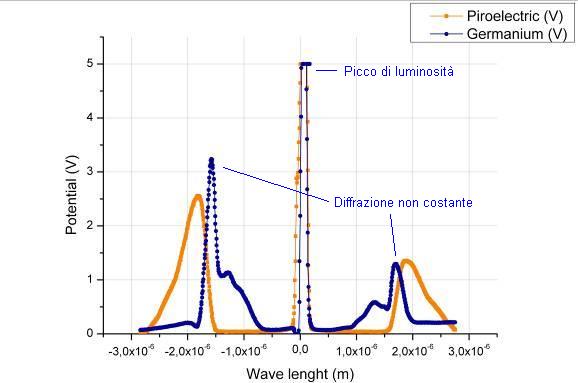
7 - Andamento dei potenziali in funzione della lunghezza d'onda della luce

Il grafico presenta due variazioni del comportamento del campione di germanio (una per angoli positivi e una per angoli negativi):

• segnale piroelettrico forte, germanio debole: i fotoni attraversano il campione, senza alterarne i livelli energetici interni, e arrivano alla superficie del sensore piroelettrico. Questo perché l’energia dei fotoni non è sufficiente a promuovere elettroni in banda di conduzione ( ).
• segnale piroelettrico debole, germanio forte: i fotoni hanno energia sufficiente per provocare l’effetto fotoelettrico interno, cioè sciogliere il legame tra elettroni di valenza e nucleo atomico inviandoli nella banda di conduzione ( ).

Le zone in cui le due curve invertono le loro tendenze e si intersecano sono utili a determinare il livello di soglia dell’energy gap.

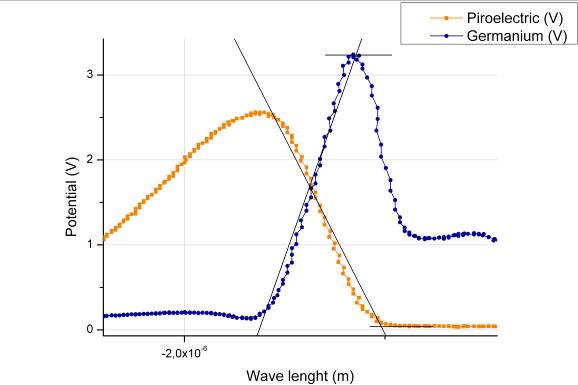
8 - Particolare del primo punto di intersezione

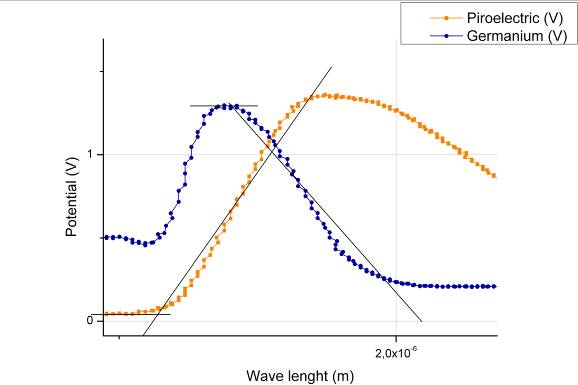
9 - Particolare del secondo punto di intersezione

I valori dell’energy gap si ottengono studiando gli intervalli dove il sensore piroelettrico e il campione si “scambiano” i potenziali. Come si nota dal grafico, ad un innalzamento del potenziale al campione si accompagna un abbassamento dello stesso al sensore piroelettrico. Tracciando una retta passante per il punto di massimo potenziale del campione e determinando la retta di regressione lineare, per i valori nell’intervallo tra il potenziale massimo e il potenziale minimo, si ottiene la prima soglia dell’energy gap. Facendo lo stesso per il sensore piroelettrico (tracciando però una retta passante per il punto di minimo potenziale) si ottiene un’altro punto dall’intersezione tra la retta di regressione e la retta passante per il minimo.

Nel caso del germanio i punti sono:

A (-1,57113757·10^-6;3,23794493);

B (-1,51168283·10^-6;0,0384507141);

C(1,56984191·10^-6;0,0395196901);

D(1,70356·10^-6;1,29034525).

Le ascisse di questi punti sono le lunghezze d’onda (espresse in m) del fascio di luce monocromatico; convertendole in energie (espresse in eV) si ottiene:

La media dei valori trovati è:

l’errore è:

dunque il valore estrapolato è: , risultato comparabile con i valori standard reperibili nei testi scientifici (E_G=0,77eV).

Lo stesso procedimento per il campione di silicio ha prodotto un risultato molto vicino ai valori di riferimento (_G=1.1 eV):

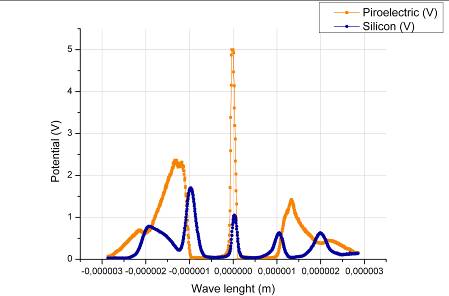
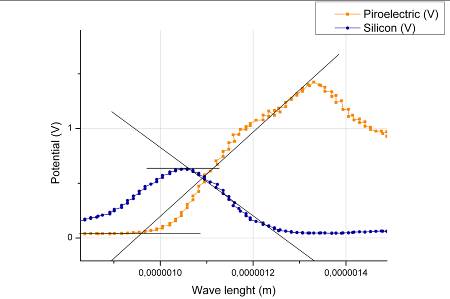
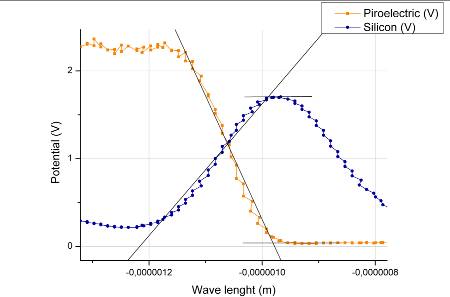
10 - Grafico e particolari dell'andamento dei potenziali in funzione della lunghezza d'onda

Bibliografia

A. Caforio, A. Ferilli, Nuova Physica 2000 volume 3, Le Monnier

S. Grove, Fisica e tecnologia dei dispositivi a semiconduttore, Ingegneria elettrica Franco Angeli Editore

P. Pistarà, Moduli di chimica, Atlas

R. Bigoni, Note didattiche, www.robertobigoni.it

R. Fieschi, R. Roncaglia, Dal silicio al computer, Istituto Nazionale Fisica Materia Media

D. Cavalcoli, I metalli e i semiconduttori, le proprietà elettriche, Università di Bologna, Dipartimento di Fisica