Quesito 1

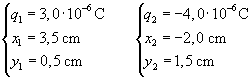
Le cariche e le coordinate di due particelle nel piano xy sono:

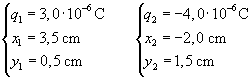
Determinare:

1. la forza F₂ agente su q₂;
2. dove dovrebbe essere posta una terza carica q₃ = 4,0·10^-6C affinché la forza totale F₂ su q₂ sia nulla.

Svolgimento

Quesito 2

Due particelle aventi la stessa carica, inizialmente distanti 3,2·10^-3m, sono lasciate libere. Si nota che l’accelerazione di una particella è di 7,0 m/s² e quella dell’altra è di 9,0 m/s².

Se la massa della prima particella è di 6,3·10^-7kg, quale è la massa della seconda? Quanto è la carica di entrambe?

Svolgimento

Quesito 3

Una carica q è distribuita uniformemente lungo una circonferenza di raggio a.

1. Calcolare il campo E per i punti che si trovano su una retta r perpendicolare al piano della circonferenza, passante per il suo centro e a distanza x da questo.
2. Si studi il moto di un elettrone che inizialmente si trova fermo a piccola distanza x sulla retta r.

Svolgimento

Quesito 4

Un protone ruota con una velocità v = 3,0 · 10⁵m/s appena fuori da una sfera carica di raggio r = 10^-6m.

Qual è la carica della sfera?

Svolgimento

Svolgimento del quesito 1

1. Le posizioni delle due cariche sono date dai vettori

   

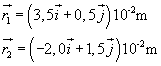
   Il vettore radiale (applicato a q₁) r = r₂ - r₁ risulta . Il suo modulo è e il suo versore è .

   Indicando sinteticamente con K il valore della costante nella forza coulombiana

   

   la forza di Coulomb agente su q₂ risulta

   

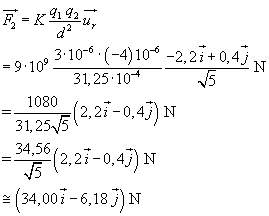
2. La forza esercitata da q₃ su q₂ deve avere modulo uguale a quello di F₂. Indicando con r' la distanza di q₃ da q₂ si ha

   

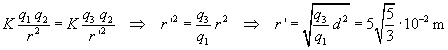
   La carica q₃ deve essere situata sulla retta passante per q₁ e q₂, dalla parte opposta di q₁ rispetto a q₂, a distanza r' da q₂.

   r' è il modulo del vettore r₃-r₂ che ha lo stesso versore di r₂-r₁ cioè u_r. Dunque

   

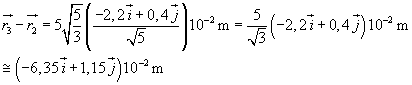
   In conclusione

   

Svolgimento del quesito 2

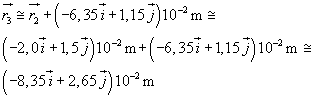
È evidente che forze e accelerazioni delle due particelle hanno uguale direzione e verso opposto.

Per il secondo principio della dinamica le accelerazioni sono inversamente proporzionali alle masse: limitandosi a considerare i moduli

La forza coulombiana agente sulla prima particella è uguale al prodotto della sua massa per la sua accelerazione. Indicando con d la distanza tra le particelle:

Svolgimento del quesito 3

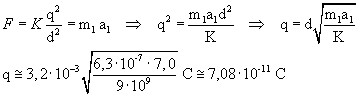
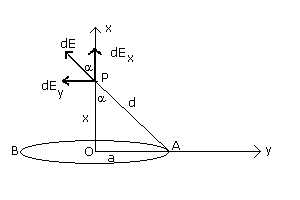
1. Indicando con dq l'elemento infinitesimo di carica presente nel punto A, il contributo dE che esso fornisce al campo nel punto P risulta in modulo:

   

   Di questo contributo risulta efficace solo la componente x in quanto la componente y è neutralizzata dalla componente y opposta del contributo al campo totale dato dalla carica uguale dq situata nel punto B simmetrico ad A. La componente x risulta

   

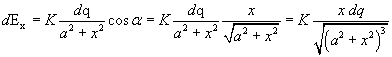
   Il campo totale nel punto P ha quindi solo la componente x e il suo modulo si ottiene integrando su tutta la carica presente sulla circonferenza:

   

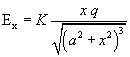
2. Nel centro O della circonferenza il campo è nullo e qualunque carica posta in O è in equilibrio: una carica positiva è in equilibrio instabile, una carica negativa è in equilibrio stabile in quanto sottoposta ad una forza sempre diretta verso O. In particolare, se il modulo di x è molto minore di a, la forza F che agisce su un elettrone risulta

   

   F è di tipo elastico e l'elettrone oscilla con moto armonico attorno ad O.

Svolgimento del quesito 4

Per il teorema di Gauss il campo di una sfera carica fuori dalla sfera stessa coincide con quello che sarebbe prodotto da una uguale carica puntiforme situata nel centro della sfera, cioè con il campo coulombiano.

Perché il protone percorra un'orbita circolare con velocità costante deve essere soggetto ad una forza centripeta costante dovuta alla sua interazione con la carica contenuta nella sfera. Il versore di questa forza è opposto al versore radiale u_r.

Indicando con e la carica del protone, con m la sua massa e con Q la carica della sfera, uguagliando le parti scalari delle forze, si ha

Con i dati forniti e ricordando che C≈9·10⁹ N·(m/C)², che m≈1,672·10^-27Kg e che e≈1,602·10^-19 C, si ha