.
Calcolare il flusso di campo elettrico:Su una superficie conduttrice piana infinita Σ posta nel vuoto c'è una densità
superficiale di carica costante
.
Calcolare il flusso di campo elettrico:
avente due facce parallele a Σ e tagliata a mezzo da Σ;
situata interamente dalla stessa parte rispetto a Σ e il cui piano è inclinato di
60° rispetto a Σ;
tagliata a mezzo da Σ;
Su un filo conduttore rettilineo e di lunghezza infinita posto nel vuoto c'è una densità
lineare di carica costante
.
Calcolare il flusso di campo elettrico:
distante L/2 dal filo messa in modo che la
perpendicolare al suo centro passi per il filo;
con quattro facce parallele al filo e messa in modo che il filo passi per il suo centro;
Si può ragionare in due modi sostanzialmente equivalenti.
La carica Q contenuta dentro al cubo è data dal prodotto della densità superficiale di
carica su Σ per la superficie S intercettata su Σ dal cubo:
.
Per il teorema di Gauss il flusso di campo elettrico uscente dalla superficie cubica è
Il campo elettrico nei dintorni di Σ è costante, perpendicolare a Σ, uscente
da essa e di modulo
.
Attraverso alle facce perpendicolari a Σ non c'è flusso, mentre attraverso ad ognuna
delle due facce parallele il flusso di campo elettrico vale
.
Il flusso totale è quindi
.
La normale al quadrato forma un angolo di 60° con il vettore di campo elettrico costante. Il flusso di E è dato dal prodotto scalare del campo per la superficie quadrata, cioè dal prodotto dei moduli di campo e area del quadrato per il coseno dell'angolo tra il vettore di campo e la normale alla superficie. In definitiva:
.
Anche qui, come nel caso del cubo, si può procedere in due modi.
La carica Q contenuta nella sfera è data dal prodotto della densità superficiale di
carica su Σ per la superficie S intercettata su Σ dalla sfera:
.
Per il teorema di Gauss il flusso di campo elettrico uscente dalla superficie sferica è
Il flusso di campo elettrico attraverso ad ognuna delle semisuperfici sferiche delimitate da Σ è identico a quello attraverso ad un cerchio di ugual raggio R. Dunque
.
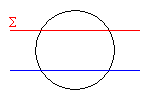
Anche qui, come nei casi precedenti, si può procedere in due modi.
Con riferimento alla figura che rappresenta una sezione del sistema con Σ
rappresentato in rosso, si osserva che la sfera intercetta su Σ un cerchio
di raggio
e quindi di area
.
Dunque la carica contenuta nella sfera è
e, per il teorema di Gauss,
.
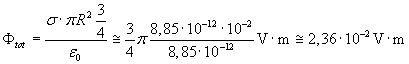La zona di superficie sferica compresa tra Σ e la superficie
piana ad essa simmetrica rispetto al centro della sfera (rappresentata in blu)
non dà nessun contributo al flusso in quanto il flusso entrante e quello uscente
sono uguali in modulo. Il flusso totale è dato dalla somma dei flussi attraverso alle calotte
esterne alle due superfici e coincide con quello attraverso alle basi della calotte stesse.
Queste basi sono cerchi di raggio
e quindi di area
.
Dunque il flusso totale è
.
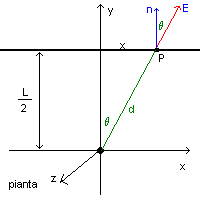
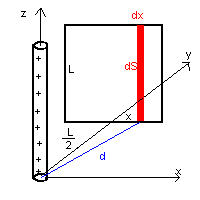
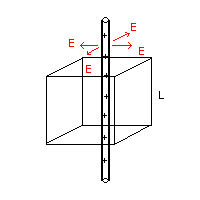
Il campo E in un punto P nei dintorni del filo (rappresentato in pianta nella prima figura
come un cerchietto nell'origine degli assi) è radiale con modulo inversamente proporzionale alla
distanza d dal filo secondo la legge
.
Indicando con θ l'angolo tra il vettore E e la normale al quadrato
(rappresentato in pianta nella prima figura),
la distanza di una striscia dS di quadrato, parallela al filo, di lunghezza L e
larghezza dx, risulta
.
Si ha inoltre
.
Il flusso di campo elettrico attraverso una striscia risulta quindi
.
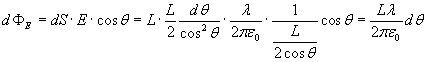Il flusso totale attraverso alla superficie quadrata si ottiene integrando:
.
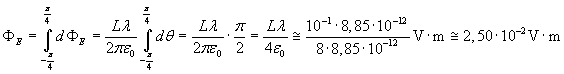Per le facce perpendicolari al filo non c'è flusso di campo elettrico. Per ognuna delle quattro facce parallele ad esso il flusso è uguale a quello calcolato al punto precedente. Quindi
.
Tutto il calcolo risulterebbe tuttavia molto più semplice ed immediato partendo dal secondo quesito e deducendo quindi la risposta al primo.
Per il teorema di Gauss il flusso attraverso alle pareti del cubo è dato dal rapporto tra la carica interna e la permittività:
.
Per trovare il flusso su una sola delle quattro facce del cubo, data la simmetria del sistema, basta dividere per quattro.