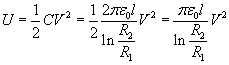Quesito 1

In un riferimento cartesiano ortogonale Oxyz c'è un campo elettrostatico di potenziale con a e b costanti note. Si consideri nel quadrante delle coordinate positive il volume del cubo di spigolo l con un vertice nell'origine e con i tre spigoli concorrenti in tale vertice posti sugli assi cartesiani.

1. Esprimere il valore del campo elettrico nel vertice più distante dall'origine.
2. Calcolare l'energia contenuta in tale volume.

Svolgimento

Quesito 2

Un condensatore cilindrico è lungo l , le sue armature coassiali hanno raggi R e 3R, tra di esse c'è, nel vuoto, una differenza di potenziale V.

1. Calcolare l'intensità del campo elettrico nei punti equidistanti dalle armature.
2. Calcolare la quantità di energia elettrostatica contenuta nel condensatore.

Svolgimento

Svolgimento del quesito 1

1. Dato che il potenziale di un punto del campo dipende solo dall'ascissa il campo risulta

   

   In particolare, l'ascissa del vertice più distante dall'origine è l e quindi in questo punto il campo vale

   

2. La densità di energia del campo elettrico è espressa da

   

   e quindi l'energia contenuta in un volume dV risulta

   

   

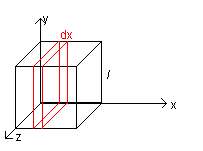
   Scegliendo come volume infinitesimo dV una sezione del cubo parallela al piano yz e di spessore dx si ha e quindi

   Per ottenere l'energia totale si integra dU da 0 a l

   

Svolgimento del quesito 2

1. La differenza di potenziale tra le armature del condensatore risulta, in modulo

   

   Ricavando λ si ha

   

   e quindi l'intensità del campo elettrico in funzione della distanza r dall'asse del condensatore risulta

   

   In particolare, in un punto distante 2R dall'asse si ha

   

2. Dall'espressione di E(r) si ottiene la densità di energia del campo tra le armature

   

   L'energia dU contenuta in un tubo di raggio r e spessore dr, coassiale con le armature e lungo come il condensatore, risulta

   

   L'energia contenuta tra R e 3R è data dall'integrale

   

   Si può ottenere più direttamente lo stesso risultato usando l'espressione della capacità di un condensatore cilindrico

   

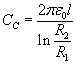
   unita all'espressione del lavoro di carica di un condensatore, che coincide con l'energia accumulata in esso