Quesito 1

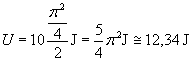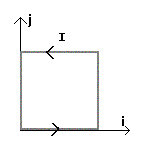
Una spira quadrata, di lato L=12 cm, resistenza R=3Ω e induttanza trascurabile, è immersa in un campo di induzione magnetica uniforme , perpendicolare al piano della spira; l'intensità di cresce nel tempo, a partire da un valore nullo nell'istante iniziale. Si osserva che nella spira circola una corrente indotta antioraria di intensità costante . Con riferimento al sistema di assi della figura, determinare:

1. il versore di , giustificando la risposta;
2. l'intensità di all'istante t₁=15s.

Svolgimento

Quesito 2

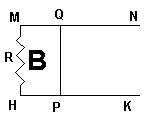
Un circuito elettrico è costituito da due conduttori paralleli HK e MN, distanti d=1m l'uno dall'altro e collegati tra loro da due conduttori ad essi perpendicolari. Il conduttore HM è fisso ma PQ è mobile e la sua distanza x da HM varia nel tempo secondo la legge con . Il ramo HM ha resistenza R=10Ω, gli altri rami hanno resistenza trascurabile. Il circuito è immerso in un campo di induzione magnetica di direzione costantemente perpendicolare al piano del circuito stesso e intensità variabile nel tempo . Calcolare:

1. il valore massimo del modulo della corrente elettrica nel circuito;
2. l'energia elettrica dissipata dalla resistenza R durante il primo secondo di attività del circuito.

Svolgimento

Svolgimento del quesito 1

1. La corrente indotta è antioraria, anche la f.e.m. indotta è antioraria, cioè positiva. La f.e.m. ha segno opposta a quello della derivata di Φ_B rispetto al tempo, dunque Φ_B cala e, dato che la superficie della spira è costante e l'intensità di B è crescente, questa intensità cresce in senso opposto a quello della normale alla spira. Il versore di B è -k.

   Ragionando in termini più 'fisici' si può anche dire che la corrente indotta, per la 'regola della mano destra', genera un campo B' che nei punti del piano xy è normale al piano stesso. Φ_B' è quindi positivo e, dato che Φ_B' si oppone alla variazione del flusso inducente Φ_B, quest'ultimo sta calando, ovvero B sta aumentando in verso opposto alla normale al piano xy e quindi il suo versore è -k.

2. Dall'equazione di Faraday, limitatamente ai moduli, si ha

   

   dove S è la superficie costante della spira. In particolare, per t=15 s, si ottiene

   

Svolgimento del quesito 2

Entrambi i quesiti sono indipendenti dal verso di B e ci si può limitare a considerare i moduli.

1. Il modulo di Φ_B concatenato con il circuito risulta

   

   Per l'intensità della corrente si ha

   

   Il valore massimo I_M dell'intensità della corrente si ha ovviamente quando il il modulo del seno vale 1 e risulta

   

2. La corrente I(t) è una funzione sinusoidale di pulsazione

   

   e il suo periodo è quindi

   

   In un secondo ci sono esattamente 5 periodi. Per calcolare l'energia dissipata sarà sufficiente moltiplicare la potenza media per la durata. Poiché il valor medio del quadrato del seno è 1/2, la potenza media risulta

   

   In definitiva l'energia dissipata in un secondo è