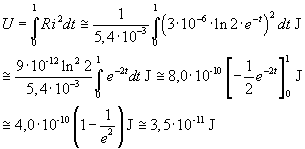fig1000 Una spira quadrata ABCD, di lato fig001, è formata da un filo cilindrico di rame di diametro fig002. La resistività del rame è fig003.

1) Calcolare la resistenza della spira.

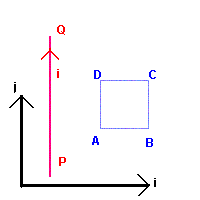
Un lungo filo conduttore rettilineo PQ, situato sul piano [i , j] della spira, parallelo al lato AD della stessa, distante l da AD, è percorso da una corrente i (con verso da P a Q) di intensità variabile nel tempo secondo la legge fig004.

Facendo riferimento al sistema di assi di figura e trascurando il coefficiente di autoinduzione della spira:

2) esprimere (in funzione del tempo) il vettore di induzione magnetica B prodotto nel centro della spira dalla corrente che circola nel filo PQ;
3) esprimere (in funzione del tempo) il flusso di B attraverso la superficie piana delimitata dalla spira (orientata come k);
4) esprimere (in funzione del tempo) l'intensità della corrente indotta nella spira;
5) calcolare l'energia dissipata in calore nella spira nell'intervallo di tempo tra 0 e 1 secondo.

Svolgimento

  1. Il raggio della sezione del filo che forma la spira è fig005, la spira è lunga 4l. Per la seconda legge di Ohm, la resistenza della spira è

    fig006

  2. Il centro della spira ha distanza c=1,5 l dal filo. Per la legge di Biot-Savart, in questo punto l'induzione magnetica B ha modulo

    fig007

    Per la 'regola della mano destra' il vettore B entra nel piano della figura, dunque ha versore -k. Il definitiva l'espressione del vettore B nel centro della spira è

    fig008

  3.  

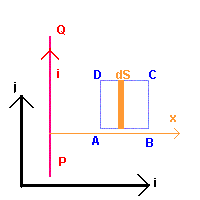    fig1001 Per calcolare all'istante t il flusso di B concatenato con il quadrato delimitato dalla spira conviene suddividere la superficie in elementi infinitesimi dS, costituiti da rettangoli di base dx a altezza l, tali che in tutti i loro punti il prodotto scalare fig009 dipenda solo da x, distanza del rettangolo dal filo, e quindi integrare dΦB da l a 2l

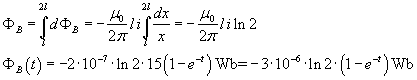
    fig010

  4. La corrente indotta nella spira, per la legge di Faraday-Lenz, è data da

    fig011

    Questa corrente circola in senso antiorario e tende asintoticamente a 0.

  5. L'energia elettrica dissipata per effetto Joule si ottiene integrando la potenza P=Ri2 rispetto al tempo

    fig012