Problema 1

Si consideri la zona dello spazio nella quale sono entrambe positive le ascisse e le ordinate di un sistema di riferimento cartesiano Oxyz. Solo in tale regione è presente un campo magnetico uniforme .

Un elettrone penetra nel campo magnetico nel punto di posizione , con velocità . Calcolare

1. il valore della costante b perché l'elettrone esca dal campo magnetico con velocità ;
2. assunto tale valore di b, quale campo elettrico bisogna sovrapporre al campo magnetico perché l'elettrone si muova (nella regione data) di moto rettilineo uniforme, con velocità ;
3. il lavoro fatto dal campo elettrico.

(assumere per la massa dell'elettrone , e per la sua carica )

Svolgimento

Problema 2

Due circuiti rettangolari sono complanari e disposticome in figura; la lunghezza dei fili è molto grande rispetto a d. Calcolare, in funzione di d e trascurando gli effetti di bordo, il coefficiente di mutua induzione per unità di lunghezza del sistema.

Svolgimento

Problema 3

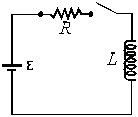
Si consideri il circuito di figura, nel quale . All'istante iniziale viene chiuso l'interruttore.

Calcolare, nei primi 2 secondi:

1. l'energia fornita dalla batteria;
2. quanta di questa energia viene immagazzinata nel campo magnetico;
3. quanta di questa energia viene dissipata nel resistore.

Svolgimento

Svolgimento del problema 1

1. L'elettrone, entrando nel campo magnetico, è sottoposto alla forza di Lorentz costantemente perpendicolare alla sua velocità. La forza di Lorentz non fa lavoro sull'elettrone e quindi il modulo delle velocità è costante. Se il campo magnetico è costante, anche il modulo della forza di Lorentz si mantiene costante: questa forza funge da forza centripeta costante, l'elettrone percorre un arco di traiettoria circolare su un piano perpendicolare al versore di B, cioè, nel caso proposto, il piano xy. Perché l'elettrone esca dal campo con la velocità finale indicata, il raggio della traiettoria deve essere R=1 m. si ha quindi

   

2. Perché l'elettrone si muova di moto rettilineo uniforme, la forza elettrostatica deve essere costantemente opposta alla forza di Lorentz:

   

3. La forza elettrostatica è opposta alla forza di Lorentz. La forza di Lorentz non fa lavoro, dunque nemmeno la forza elettrostatica fa lavoro. Quindi il lavoro del campo elettrico è nullo. Si può anche dire che, dato che per ipotesi il modulo della velocità dell'elettrone è costante, la sua energia cinetica non cambia: per il teorema delle forze vive, il lavoro della risultante delle forze che agiscono su di esso è nullo, e, dato che il lavoro della forza di Lorentz è nullo, anche quello del campo elettrico è nullo.

Svolgimento del problema 2

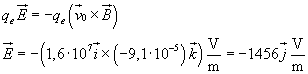
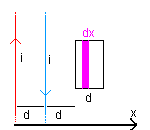
Considerando i fili del circuito superiore come rettilinei e di lunghezza infinita, il modulo del campo magnetico generato dalle correnti che li percorrono può essere calcolato con la legge di Biot-Savart. Nei due fili le correnti hanno identica intensità ma verso opposto. Assumendo come origine la posizione del primo filo, in un punto del piano contenente i due fili a destra del secondo filo il modulo dell'induzione magnetica risulta

Considerando un tratto lungo 1 m del secondo circuito, il modulo del flusso concatenato con una striscia di larghezza infinitesima dx risulta

e il modulo del flusso di B per unità di lunghezza risulta

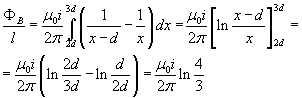
Il coefficiente di mutua induzione per unità di lunghezza è quindi

Svolgimento del problema 3

Per una nota proprietà dei circuiti RL alimentati da una f.e.m. costante ε la corrente ad un istante t dopo la chiusura del circuito risulta

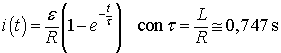
1. L'energia erogata dall'alimentatore nei primi due secondi è

   

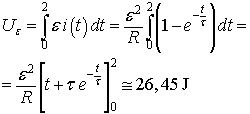
2. L'energia incamerata nel campo magnetico al tempo t è

   

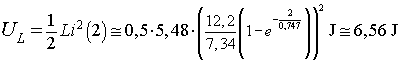
3. L'energia dissipata per effetto Joule è data dalla differenza tra i valori precedentemente calcolati