Problema 1

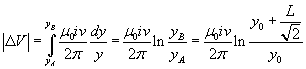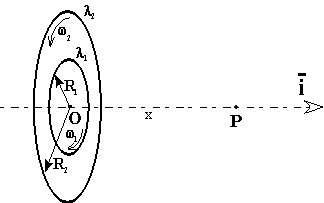
Due anelli non conduttori, piani e concentrici, aventi raggio R₁ e R₂, portano, ciascuno, una carica positiva distribuita uniformemente con densità lineare λ. I due anelli ruotano attorno all'asse i, perpendicolare al piano dei due anelli e passante per il loro centro O, con velocità angolari identiche in modulo (ω) ma in versi opposti, come indicato in figura.

Determinare:

1. il campo elettrico E nel punto P dell'asse i distante x₀ da O;
2. il campo magnetico B nel punto P;
3. il momento di dipolo magnetico totale associato ai due anelli.

Una piccola particella di dimensioni trascurabili, avente massa M_a, che possiede una carica q_a ed un momento di dipolo magnetico m_a, viene posta (in quiete) nel punto P e poi lasciata libera di muoversi.

Determinare:

1. la velocità della particella quando essa giunge in O.

Svolgimento

Problema 2

Un filo conduttore rettilineo, molto lungo, giace lungo l'asse delle ascisse; esso è percorso da una corrente di intensità i, che fluisce nel verso positivo di tale asse. Una sbarra AB, sottile e conduttrice, di lunghezza L, viene posta lungo la retta y=x, nel quadrante di ascisse e ordinate positive, con l'estremo più vicino situato a distanza y₀dal filo.

In un determinato istante la sbarra viene messa in movimento, a una velocità di modulo v costante, in traslazione parallela alla corrente.

Si determini

1. la differenza di potenziale fra gli estremi della sbarra, in regime stazionario.

Svolgimento

Svolgimento del problema 1

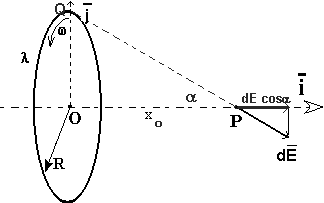
1. Scelto un punto Q di un anello di raggio R, si assuma un sistema di riferimento cartesiano con assi OP e OQ. Indicato con dl un tratto infinitesimo di anello centrato su Q, dl contiene una carica che genera nel punto P un campo

   

   dove il versore u_r indica la direzione radiale da Q a P. L'unico componente efficace di questo campo è quello di verso i in quanto il componente di verso j è neutralizzato dal componente opposto del campo generato dalla carica simmetrica a quella in Q rispetto ad O. In definitiva la componente efficace del campo generato dalla carica in Q è data dal prodotto del modulo del campo per il coseno dell'angolo QPO. Il campo efficace è quindi

   

   Integrando su tutta la lunghezza L=2πR dell'anello, il campo totale prodotto in P dalla carica presente su un anello è

   

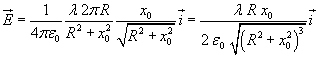
   Dato che ci sono due anelli di raggi rispettivi R₁ e R₂, il campo prodotto in P risulta

   

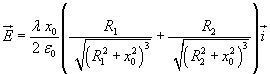
2. Una spira circolare di raggio R percorsa da una corrente i genera in un punto P del suo asse, distante x₀ dal suo centro O, un campo di induzione magnetica assiale B di modulo

   

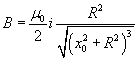
   B è diretto verso O se la corrente, vista da P, è oraria; altrimenti B ha verso opposto.

   La rotazione di un anello con velocità angolare di modulo costante ω produce una corrente di intensità

   

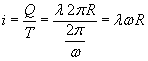
   In definitiva, sommando i contributi all'induzione magnetica in P dovuti alla rotazione dei due anelli, si ottiene

   

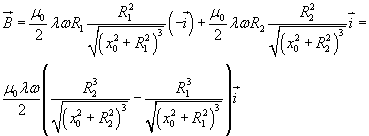
3. Il momento magnetico dovuto a una corrente positiva (antioraria) i che percorre una spira piana di area S è perpendicolare al piano della spira e ha intensità m = i S. Nel nostro caso si è visto che i=λ ω R; l'area della spira è S = π R². Quindi . Sommando i momenti delle due spire (dovute alla rotazione dei due anelli) si ottiene

   

4. Una carica infinitesima λdl, posta su un anello di raggio R, genera nel punto P dell'asse, distante x_o da O, un potenziale elettrico

   

   Il potenziale totale prodotto da tutta la carica distribuita sull'anello è quindi

   

   Il potenziale elettrico nel centro O della spira (ascissa=0) risulta

   

   Sommando i potenziali prodotti dai due anelli si ottiene, nei due casi,

   

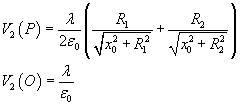
   L'energia potenziale elettrica di una particella di carica q_a risulta quindi, nei due casi

   

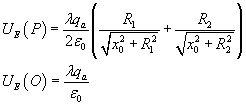
   Nello spostamento da P a O la particella ha una variazione di energia potenziale elettrica

   

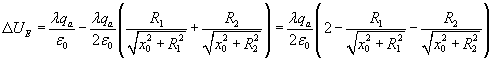
   In quanto dotata di momento di dipolo magnetico, la particella, nel punto P, ha energia potenziale magnetica

   

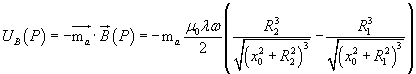
   Nel punto O l'energia potenziale magnetica della particella è nulla, quindi la variazione di energia potenziale magnetica nel passaggio da P a O risulta

   

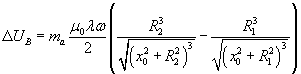
   La diminuzione di energia potenziale della particella implica un aumento della sua energia cinetica, inizialmente nulla. In O si ha quindi

   

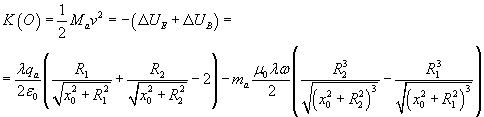
   In definitiva

   

Svolgimento del problema 2

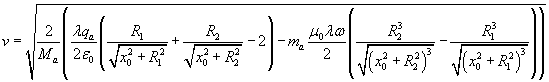
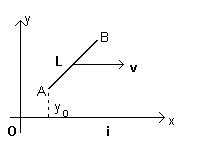
1. Su ogni tratto infinitesimo dl della sbarra conduttrice, posto a distanza y dalla corrente e contenente una carica dq, per la legge di Biot-Savart, agisce un campo di induzione magnetica B

   

   Sulla carica dq che si muove con velocità v=vi agisce la forza di Lorentz

   

   Per effetto di tale forza ogni carica dq subisce uno spostamento

   

   Il lavoro della forza di Lorentz sulla carica è quindi

   

   e la differenza di potenziale prodotta, in modulo,

   

   Il modulo della differenza di potenziale tra A e B si ottiene integrando tra le ordinate di A e B