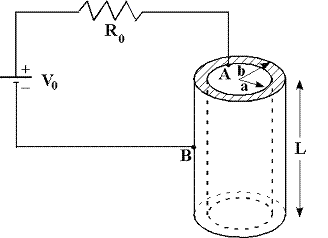
Un condensatore cilindrico ha lunghezza L = 10 cm, armatura interna di raggio a = 5 mm ed armatura esterna di raggio b = 7 mm. Lo spazio tra le due armature è interamente riempito, inizialmente, con un materiale omogeneo avente una resistività ρ = 10 Ω·m e costante dielettrica relativa εr=1,5.
Il condensatore viene inserito nel circuito elettrico di figura, con l'armatura interna del condensatore collegata al punto A del circuito e quella esterna al punto B.
In tale situazione, con Vo = 100 Volt ed Ro=50Ω, determinare, in condizioni stazionarie e trascurando gli effetti dei bordi:
Solo dopo aver risposto alle precedenti domande.
Si supponga ora di estrarre il materiale presente tra le armature del condensatore. Determinare:
(N.B. : si ricorda che il condensatore di figura può essere schematizzato con una resistenza posta in parallelo ad una capacità).
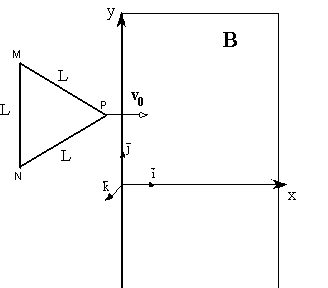
Una spira di materiale conduttore a forma di triangolo equilatero, di lato L = 20 cm e
di resistenza complessiva R = 0,25 Ω, si trova nel piano xy di figura, con un lato
parallelo all'asse y. All'istante t = 0, essa inizia a penetrare in una regione di spazio
(vuoto) in cui vi è un campo magnetico uniforme con induzione magnetica
,
limitatamente alla regione x > 0.
Nell'ipotesi che la spira venga sempre mantenuta a velocità costante
,
calcolare, trascurando ogni fenomeno di autoinduzione:
Solo dopo aver risposto alle precedenti domande, calcolare:
.
1
La capacità del condensatore, quando tra le armature c'è il vuoto, è
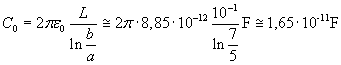
Quando il condensatore è 'riempito' la sua capacità risulta
La resistenza del condensatore 'riempito' è
La resistenza totale del circuito risulta
Nel circuito, a regime, circola una corrente costante
In questa condizione, ai capi del condensatore c'è una differenza di potenziale
L'energia immagazzinata nella capacità risulta quindi
2
La carica sulle armature, in valore assoluto, è
La densità chiesta si ottiene dividendo la carica per la superficie (laterale) del cilindro
3
A regime la corrente è costante e quindi anche la potenza dissipata dalla resistenza R0 è costante. Per il calcolo dell'energia dissipata si moltiplica la potenza per il tempo di attività
4
Se il condensatore è vuoto, a regime non si ha conduzione. In questo caso la differenza di potenziale ai capi del condensatore è V0 e l'energia immagazzinata nella capacità è
La variazione richiesta si ottiene dalla differenza tra questo valore e quello calcolato al punto 1.
1
Per la legge di Lenz, la corrente indotta deve produrre un campo magnetico il cui flusso si opponga alla variazione del flusso del campo inducente. Il campo inducente ha flusso negativo, crescente in valore assoluto man mano la spira penetra in esso, ma calante in valore relativo; la corrente indotta deve quindi produrre flusso positivo cioè circolare in senso antiorario.
2
L'altezza del triangolo equilatero formato dalla spira è
Misurando il tempo a partire dall'istante in cui il punto P entra nel campo B,
nella spira si ha corrente indotta solo per
Per valori di t compresi in questo intervallo, indicando con x l'ascissa del
punto P, l'area della parte di spira immersa nel campo B risulta
e il flusso di B concatenato con la spira è
La corrente indotta, per la legge di Faraday, è quindi
Questa corrente ha il suo massimo per il valore massimo di t, quindi
3
L'energia dissipata si ottiene integrando la potenza rispetto al tempo
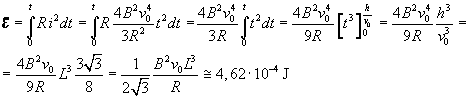
4
La potenza da applicare, per il principio di conservazione dell'energia, deve compensare
quella dissipata per effetto Joule. Questa potenza è diversa da zero solo per
.
In questo intervallo la potenza vale
e raggiunge il suo massimo per
.
In definitiva
