Problema 1

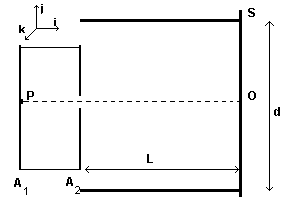
Una sorgente praticamente puntiforme emette particelle α (aventi energia ) da un punto P (vedi figura) posto all'interno di una camera a forma di parallelepipedo. Tra le due pareti verticali A₁ e A₂ viene mantenuta una differenza di potenziale . Nella parete A₂ opposta alla sorgente è praticato un piccolo foro, in modo che un fascio collimato di particelle α possa uscire dalla camera. Il fascio collimato entra poi nella regione di spazio compresa tra le armature di un condensatore, a facce quadrate piane e parallele, scarico. Il lato di tale quadrato è e la distanza tra le armature è . In tale regione esiste un campo magnetico uniforme di induzione . Al termine della regione di spazio delimitata dalle armature è posto uno schermo S, in grado di rivelare il punto di impatto del fascio di particelle α.

Determinare, trascurando ogni effetto gravitazionale:

1. L'energia cinetica posseduta dalle particelle α quando esse entrano tra le armature del condensatore.
2. La posizione, rispetto ad O, del punto Q in cui il fascio di particelle α colpisce lo schermo S.
3. Quale differenza di potenziale ΔV₂ (valore e polarità) occorrerebbe applicare tra le armature del condensatore affinché il fascio di particelle incidesse sullo schermo S nel punto O.

N.B.: le particelle α sono nuclei di elio (massa , carica ).

Soluzione

Problema 2

Le armature circolari (R=2 cm) di un condensatore piano si trovano inizialmente a distanza d=2 mm l'una dall'altra e sono connesse a una batteria da 60 V. Successivamente, a partire dall'istante iniziale, esse vengono allontanate l'una dall'altra, a velocità relativa costante di modulo v 1 mm/s.

Si assumano trascurabili le disuniformità ai bordi del condensatore e la resistenza ohmica del circuito.

Calcolare, 3 secondi dopo l'istante iniziale:

1. l'intensità della corrente di spostamento fra le armature del condensatore;
2. l'intensità del campo elettrico, fra le armature, a distanza r=1 cm dall'asse di simmetria;
3. la direzione e l'intensità del campo magnetico, nella stessa posizione.

Soluzione

Problema 1 - Soluzione

1

Nella zona A₁-A₂ le particelle subiscono un incremento di energia cinetica , raggiungendo quindi un'enegia cinetica

2

A questa energia cinetica corrisponde una velocità .

Nell'istante dell'ingresso nel campo magnetico le particelle sono soggette alla forza di Lorentz .

Questa forza, perpendicolare alla velocità, è una forza centripeta di modulo costante che incurva la traiettoria delle particelle su un arco di circonferenza con curvatura inizialmente verso il basso. Indicando con R il raggio di questa circonferenza e operando sui moduli, si ha

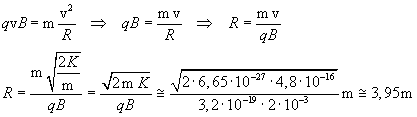
Assumendo il foro come origine, il centro della circonferenza è C(0;-R) e l'equazione della circonferenza risulta e l'equazione dello schermo .

Risolvendo il sistema delle due equazioni si trova l'ordinata del punto di incidenza del fascio sullo schermo:

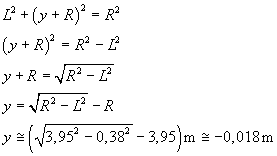
Il fascio colpisce lo schermo S circa 18mm al di sotto del punto O.

3

Se si vuole che la traiettoria del fascio nel campo magnetico sia rettilinea, bisogna 'neutralizzare' la forza di Lorentz con una forza elettrica F_e diretta verso l'alto (+j).

Operando sui moduli delle due forze si ha

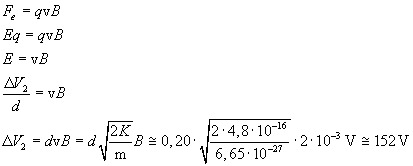
Questo potenziale cala dal basso verso l'alto.

Problema 2 - Soluzione

1

Detta V la differenza di potenziale costante tra le armature, l'intensità del campo elettrico E tra le armature varia nel tempo secondo la legge

Detta S la superficie delle armature, il flusso del campo elettrico tra le armature è quindi

La corrente di spostamento è la derivata rispetto al tempo del prodotto tra permittività e flusso di E. Nell'ipotesi che tra le armature ci sia il vuoto:

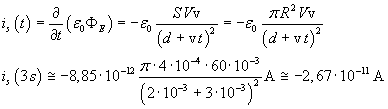
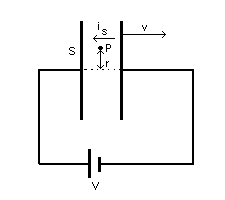
Riferendosi al circuito rappresentato in figura, tra le armature il campo è diretto verso destra. Supponendo in moto l'armatura destra, il campo cala; la sua derivata rispetto al tempo è quindi negativa: la corrente di spostamento è dunque diretta verso sinistra (segno negativo).

2

Il campo, nell'approssimazione indicata, è lo stesso in tutto il volume tra le armature. Nel punto proposto, come in ogni altro punto del volume, ha intensità

3

Il cerchio di raggio r è concatenato con la corrente di spostamento

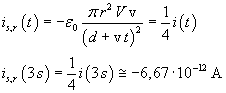
La corrente di spostamento produce gli stessi effetti magnetici di una corrente reale di uguale intensità. Per il calcolo dell'intensità di B nel punto indicato si può quindi applicare la legge di Biot-Savart:

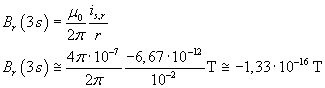
Se il punto P, ad 1 cm dall'asse di simmetria, è situato come in figura, B è entrante. Nel punto simmetrico di P rispetto all'asse di simmetria, B è uscente.