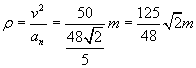Quesito 1

Dati i vettori

1. Calcolare il loro prodotto scalare e il loro prodotto vettoriale.
2. Calcolare la misura dell'angolo tra di essi.
3. Calcolare il vettore p₁₂, proiezione di v₁ su v₂.
4. Individuare nel piano xy i versori normali rispetto a v₁.

Risoluzione

a)

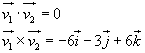
b)

Il prodotto scalare è nullo, quindi i vettori sono l'uno normale all'altro.

c)

Data la perpendicolarità dei due vettori, la proiezione chiesta è nulla.

d)

Un versore sul piano xy è un vettore

La perpendicolarità rispetto a v₁ comporta

Le soluzione del sistema

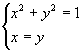
sono

Quesito 2

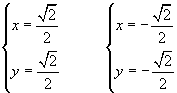
E' dato il vettore posizione r(t) definito in forma parametrica dalle equazioni

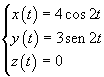
in cui tutte le grandezze sono misurate nel S.I.

1. Determinare l'equazione della traiettoria.
2. Determinare i vettori velocità e accelerazione in un generico istante t.
3. Determinare il raggio di curvatura della traiettoria nell'istante t₁=π/8 s.

Risoluzione

a)

La traiettoria è evidentemente piana. Elevando al quadrato entrambe le componenti x e y e isolando a secondo membro le funzioni trigonometriche si ha

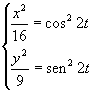
e quindi sommando membro a membro

L'equazione ottenuta è l'equazione canonica di un'ellisse di semiassi 4 e 3.

b)

Derivando le componenti della posizione rispetto al tempo si ottiene

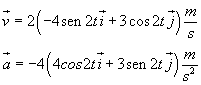
c)

Nell'istante indicato i vettori velocità e accelerazione sono

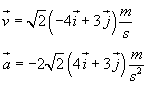
Il versore della velocità

moltiplicato scalarmente per l'accelerazione dà la componente tangenziale dell'accelerazione

Si può quindi ottenere la componente normale dell'accelerazione

e quindi il raggio di curvatura