Quesito 1

Una particella si muove sull'asse x attratta verso l'origine O con una forza proporzionale alla sua distanza istantanea da O. Se parte dalla quiete in x = 5m e raggiunge x = 2,5m per la prima volta dopo 2 s, trovare:

1. la posizione in un qualsiasi istante dopo la partenza;
2. il modulo della velocità in x = 0;
3. ampiezza, periodo e frequenza delle oscillazioni;
4. la massima accelerazione;
5. il modulo della velocità massima.

Quesito 2

Risolvere l'equazione con le condizioni x = 5, per t = 0 e, supponendo che x sia misurato in metri e t in secondi, si determini l'energia cinetica di un corpo di massa m = 10^-2 kg negli istanti t = 1s e t = 3s.

Quesito 3

E' data l'equazione per le oscillazioni smorzate di un oscillatore armonico. Si dimostri che se , allora Si dimostri, cioè, che, se vi è smorzamento, l'energia totale E diminuisce col tempo.

Svolgimento del quesito 1

Se la forza è proporzionale alla distanza, lo è anche l'accelerazione, quindi sarà:

Si tratta quindi di un moto armonico, la cui soluzione è del tipo:

dove si è tralasciata la notazione vettoriale trattandosi di un moto unidimensionale. Per determinare A, ω e φ si utilizzano le informazioni al contorno date nel testo del problema: , , .

Si ottiene il sistema:

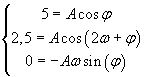
Dall'ultima equazione si ricava .

Sostituendo questi valore nella prima equazione, si determina A, che è un modulo, ottenendo A = 5 (in metri). Sostituendo, infine, i valori trovati nella seconda equazione e imponendo che ω sia positivo, si ha:

(in rad).

(in s^-1)

La legge oraria è quindi

1.  

   

2. Dall'equazione oraria si possono ricavare tutte le risposte:

   

   

3. Ampiezza: A = 5 m

   Periodo:

   Frequenza:

4.  

   

   Si ha l'accelerazione massima quando il coseno è - 1:

5. Il modulo della velocità massima è:

Svolgimento del quesito 2

L'equazione caratteristica di questa equazione differenziale omogenea del secondo ordine è:

che, avendo il discriminante Δ negativo, ammette due soluzioni complesse coniugate:

La soluzione è quindi:

Utilizzando le condizioni iniziali date si possono determinare A e B:

Quindi:

Svolgimento del quesito 3

Se , si ha:

ma da si ricava

quindi come si doveva dimostrare.