Dati il punto C(xC;yC;zC) e il numero reale positivo r, l'equazione della superficie sferica di centro C e raggio r è l'insieme dei punti P(x;y;z) con distanza r da C
Sviluppando i quadrati si ha
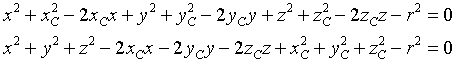
quindi un'equazione riducibile alla forma
è l'equazione di una sfera di centro
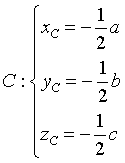
e raggio
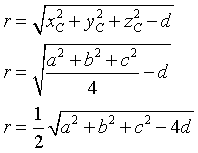
Ovviamente, la sfera è reale solo se il radicando è positivo.
Esempio.
L'equazione 
è l'equazione della sfera di centro
C(1;1;1) e raggio r=1.
Una sfera Σ e un piano Π sono tangenti se la distanza del centro C della sfera dal piano è uguale al raggio r della sfera.
Esempio.
Dato il piano Π di equazione 
, la sua distanza dall'origine è
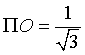, dunque l'equazione della sfera con centro in O e tangente a Π è
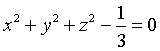
Il punto T di tangenza si può individuare calcolando le equazioni della retta parallela al versore del piano e passante per O:
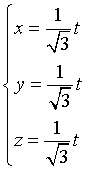
e calcolando le intersezioni di questa retta con il piano
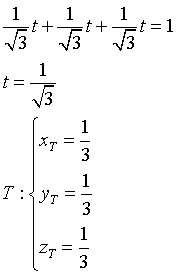
Se la distanza di C da Π è minore di r, Σ e Π si intersecano in una circonferenza.
Esempio.
Dato il piano Π di equazione , la sua distanza dall'origine è
.
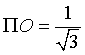La superficie sferica Σ con centro in O e raggio r=1 ha equazione
Le equazioni della circonferenza Γ, intersezione di Π e Σ sono
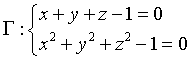
Γ è ovviamente sul piano Π; la perpendicolare a Γ per il suo centro Z passa per il centro di Σ, in questo caso O, quindi Z è il punto di intersezione della retta perpendicolare a Π per O con Π stesso. Con calcoli uguali a quelli dell'esempio precedente si ottiene
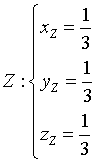
Per il Teorema di Pitagora, il raggio rΓ di Γ è
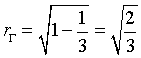
Vedere il quesito 5