Zone e calotte sferiche

Appunti per i Licei Scientifici
(da Note Didattiche)

1. Zona sferica

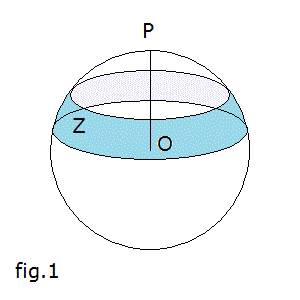
Data una superficie sferica Σ di centro O e raggio OP di misura R, due piani φ e ψ paralleli e tali che la loro distanza dal centro O sia minore di R, intersecano Σ in due circonferenze.

Si dice zona sferica Ζ  la porzione di Σ delimitata da queste circonferenze. I cerchi racchiusi da queste circonferenze sono le sue basi.

Per calcolare la superficie di una zona sferica si può procedere nel seguente modo:

• si tracci da O una perpendicolare OQ a OP;

  

• si considerino le intersezioni tra Σ, φ e ψ con il piano Π di queste due perpendicolari;

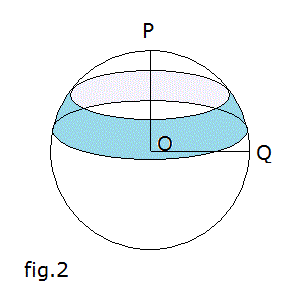
• si assume la retta OQ come asse delle ascisse e la retta OP come asse delle ordinate;

  

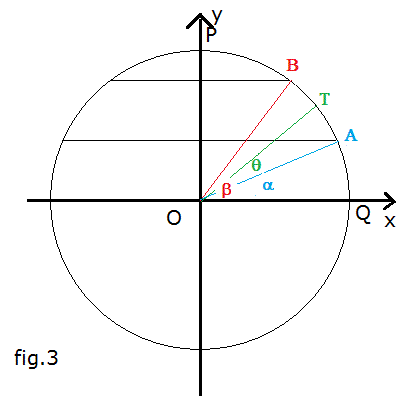
• i punti A e B sono rispettivamente le intersezioni nel primo quadrante tra γ e i piani φ e ψ; T è un punto qualunque di γ;

  i raggi OA, OB e OT formano, rispettivamente, gli angoli α, β e θ con il verso positivo dell'asse x;

  le coordinate di A, B e T sono rispettivamente

  

• un tratto infinitesimale dγ di γ ha lunghezza

  

• l'area S della zona Z si può concepire come la somma delle superfici laterali di cilindri di altezza infinitesimale dγ e raggio di base con θ da α a β;

  

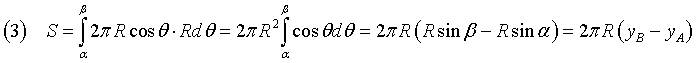
• indicando con δ la distanza tra i piani φ e ψ

  

  si ottiene

  

2. Segmento sferico

Con riferimento alla fig. 1, il solido Ω delimitato dalla zona sferica Z e dalle sue basi è detto segmento sferico.

Con riferimento alla fig. 3 e con un metodo analogo a quello usato per il calcolo di S, il volume V di Ω può essere calcolato come somma dei volumi di cilindri di altezza infinitesimale dy e raggio di base con y da y_A a y_B;

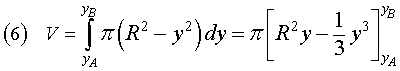
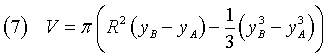
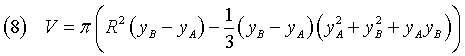
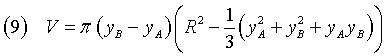
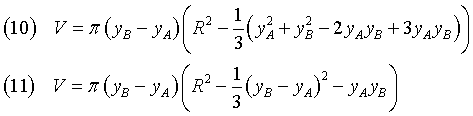
Utilizzando la (4) si ottiene

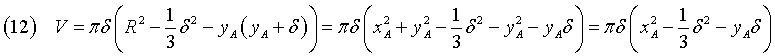
Applicando il teorema di Pitagora

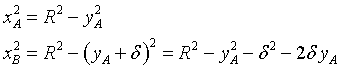
Sottraendo membro a membro

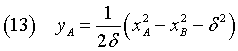
Sostituendo questa espressione di y_A nella (12)

3. Calotta sferica

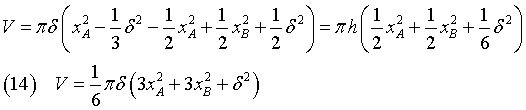
Se nella fig. 1 il piano più distante dal centro è tangente alla sfera in P, la figura risultante è detta calotta sferica.

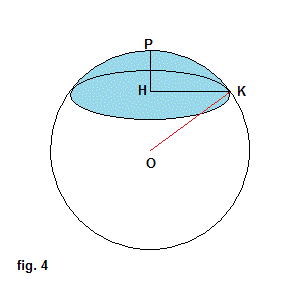
Nella fig. 4, H è il centro della sua base, P il suo vertice, il segmento HK il raggio della sua base di misura r, il segmento HP la sua altezza di misura δ e OK il raggio della sfera di misura R.

Per la superficie esterna della calotta è ancora valida la (5)

Il volume della calotta si ottiene dalla (14) con x_A=r e x_B=0.

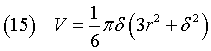
Per il teorema di Pitagora

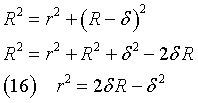
Sostituendo questa espressione di r² nella (15) si ottiene

3. Calotta visibile di una superficie sferica.

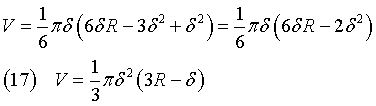
Data una superficie sferica Σ di centro O e raggio R e un punto E esterno a Σ posto a distanza h dalle stessa, la porzione di Σ osservabile da E è una calotta la cui area si può calcolare nel seguente modo:

• si considera il cono Γ con vertice in E, superficie laterale tangente a Σ e base costituita dei punti di tangenza;

• si rappresentano le intersezioni di Σ e Γ con un piano passante per la retta OE;

  

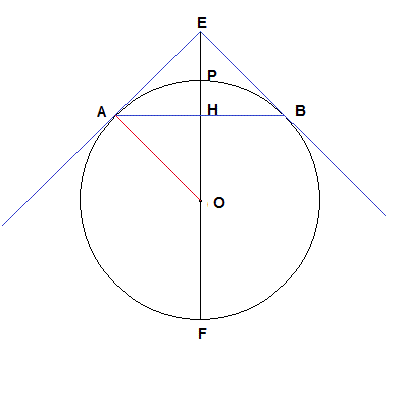
  la sezione di Σ è una circonferenza; la sezione di Γ è un triangolo isoscele di vertici E, A e B;
  l'altezza del triangolo giace sulla retta del diametro EF, interseca la circonferenza in P e interseca la base in H;

• il triangolo EAO è rettangolo in A;

• per il primo teorema di Euclide

  

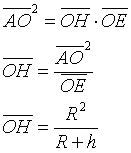
• per la calotta si ha quindi

  

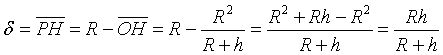
• e infine, per la (5),

  

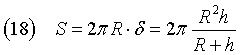
Ricordando che la superficie della sfera Σ è 4πR², risulta che la frazione di superficie sferica visibile da E è

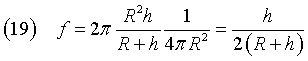
ultimo aggiornamento: 16//03/2018