Appunti per i Licei Scientifici
(da Note Didattiche)
Un'equazione di secondo grado in x e y
![]()
dove A, B, C, D, E, F sono coefficienti reali definiti a meno di una costante di proporzionalità k (k≠0) e A, B, C non sono tutti uguali a zero, rappresenta una conica.
Siano d: ax+by+c=0 l'equazione della sua direttrice, con a e b non entrambi nulli, e Φ(xΦ,yΦ) un suo fuoco.
Valgono le seguenti equazioni
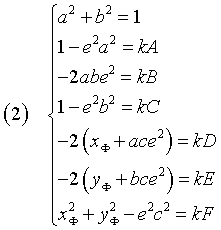
Sottraendo membro a membro la quarta delle (2) dalla seconda si ha
![]()
Per la (3), A=C ⇒ (e = 0) ∨ (a2 = b2).
Per la terza delle (2), B = 0 ⇒ (e = 0) ∨ ((a = 0) ∧ (b = 1)) ∨ ((a = 1) ∧ (b = 0)).
Dunque ((A=C) ∧ (B = 0)) ⇒ (e = 0), cioè la conica è una circonferenza e non ammette direttrice.
In questo caso la (1) si riduce alla seguente
![]()
Con la tecnica del completamento dei quadrati si ha
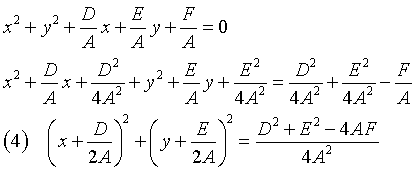
La (4) è l'equazione di una circonferenza di centro Ω e raggio ρ
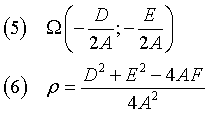
La circonferenza è reale solo se ρ è positivo.
Se (A ≠ C) ∨ (B ≠ 0), la conica non è una circonferenza e ha eccentricità positiva. Posto
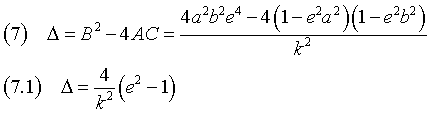
Quindi:
Con A ≠ C, mettendo la (3) a sistema con la prima delle (2)
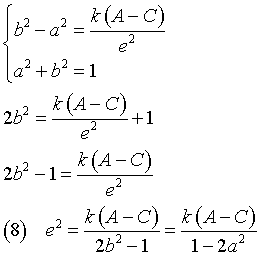
Se l'eccentricità è positiva, dalla terza delle (2), B = 0 ⇒ (((a = 0) ∧ (b ≠ 0)) ∨ ((a ≠ 0) ∧ (b = 0))
Quindi, se B = 0, la conica ha direttrice parallela a uno degli assi cartesiani.
Dalla (8)
(B = 0) ∧ (A-C > 0) ⇒ (a = 0) ∧ (b ≠ 0)
(B = 0) ∧ (A-C < 0) ⇒ (a ≠ 0) ∧ (b = 0)
3.1 Parabole
Se (B = 0) ∧ ((A = 0) ∨ (C = 0)), per la (7), la (1) è l'equazione di una parabola con eccentricità e = 1. Si hanno i seguenti casi particolari.
(A = 0) ∧ (B = 0): la (1) si riduce a
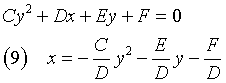
La (9) è l'equazione di una parabola con direttrice d parallela all'asse y, vertice V e fuoco Φ.
Ponendo, per semplificare la notazione,
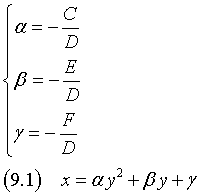
si ha
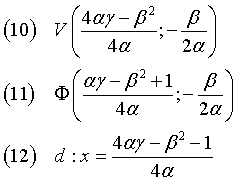
(B = 0) ∧ (C = 0): la (1) si riduce a
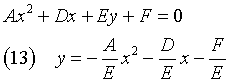
La (13) è l'equazione di una parabola con direttrice d parallela all'asse x, vertice V e fuoco Φ.
Ponendo, per semplificare la notazione,
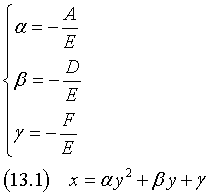
si ha
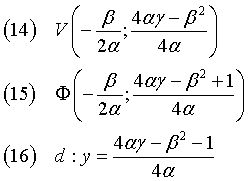
Se (B = 0) ∧ (A ≠ 0) ∧ (C ≠ 0), se (A < 0), si moltiplicano entrambi i membri della (1) per -1.
Si hanno i seguenti casi particolari.
3.2 Ellissi
Se (B = 0) ∧ (AC > 0), per la (7) la (1) è l'equazione di un'ellisse. Si hanno i seguenti casi particolari.
(B = 0) ∧ (A > 0) ∧ (C > 0) ∧ (A < C) ⇒ (a ≠ 0) ∧ (b = 0): la (1) si riduce a
![]()
La conica è un'ellisse con direttrice parallela all'asse y e asse focale parallelo all'asse x.
Completando i quadrati
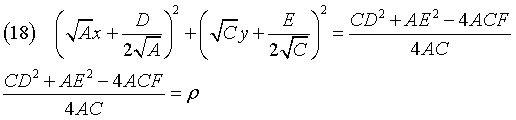
Se ρ non è positivo, l'ellisse non è reale. Altrimenti ha centro Ω e semiassi α e β
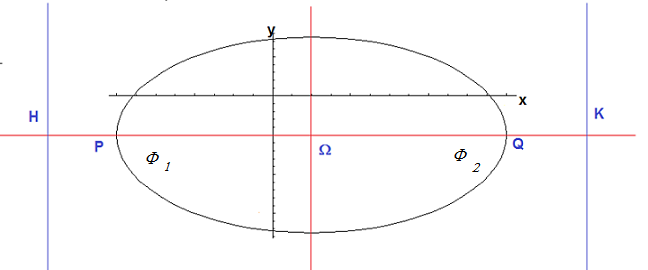
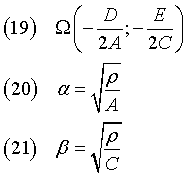
Le distanza φ dei fuochi dal centro Ω e l'eccentricità e sono
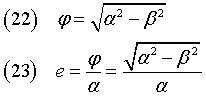
Le coordinate dei fuochi Φ1 e Φ2 sono
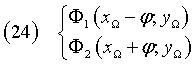
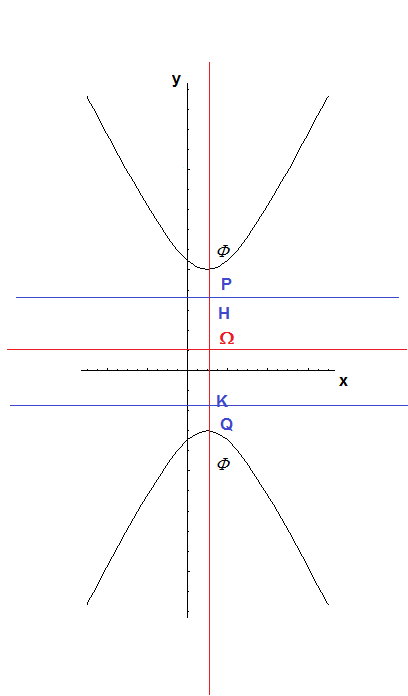
Detti P e Q i punti di intersezione della conica con l'asse focale (xP < xQ), H e K i punti di intersezione dell'asse focale con le direttrice (xH < xK), si ha
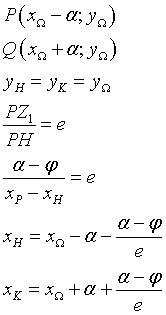
In definitiva, le equazioni delle direttrici sono
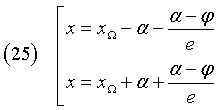
(B = 0) ∧ (A > 0) ∧ (C > 0) ∧ (A > C) ⇒ (a = 0) ∧ (b ≠ 0): la (1), come nel caso precedente, si riduce a
![]()
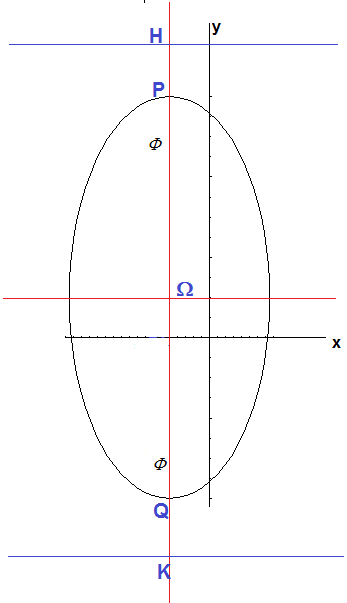
La conica è un'ellisse con direttrice parallela all'asse x e asse focale parallelo all'asse y.
Completando i quadrati
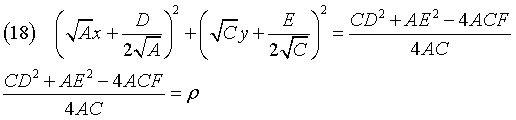
Se ρ non è positivo, l'ellisse non è reale. Altrimenti ha centro Ω e semiassi α e β
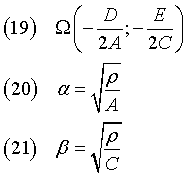
Le distanza φ dei fuochi dal centro Ω e l'eccentricità e sono
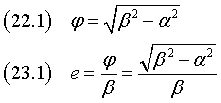
Le coordinate dei fuochi Φ1 e Φ2 sono
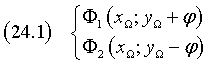
Detti P e Q i punti di intersezione della conica con l'asse focale (yP > yQ), H e K i punti di intersezione dell'asse focale con le direttrici (yH > yK), si ha
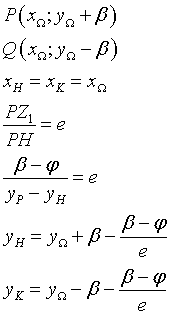
In definitiva, le equazioni delle direttrici sono
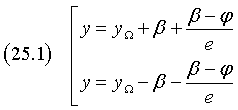
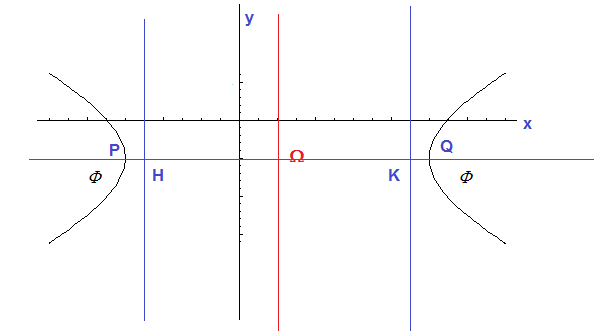
3.3 Iperboli
Se (B = 0) ∧ (AC < 0), per la (7) la (1) è l'equazione di un'iperbole. Si hanno i seguenti casi particolari.
(B = 0) ∧ (A > 0) ∧ (C < 0) ∧ (A+C < 0) ⇒ (a ≠ 0) ∧ (b = 0): la (1) si riduce a
![]()
La conica è un'iperbole con direttrice parallela all'asse y e asse focale parallelo all'asse x.
Completando i quadrati
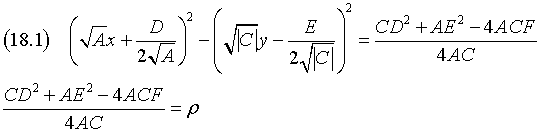
Se ρ non è positivo, l'iperbole non è reale. Altrimenti ha centro Ω e semiassi α e β
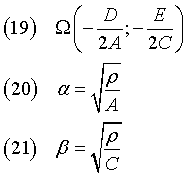
Le distanza φ dei fuochi dal centro Ω e l'eccentricità e sono
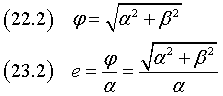
Le coordinate dei fuochi Φ1 e Φ2 sono
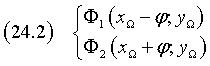
Detti P e Q i punti di intersezione della conica con l'asse focale (xP < xQ), H e K i punti di intersezione dell'asse focale con le direttrice (xH < xK), si ha
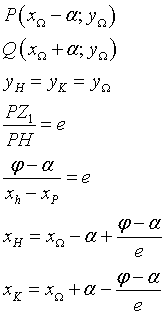
In definitiva, le equazioni delle direttrici sono
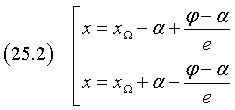
(B = 0) ∧ (A > 0) ∧ (C < 0) ∧ (A+C > 0) ⇒ (a = 0) ∧ (b ≠ 0): la (1) si riduce a
![]()
La conica è un'iperbole con direttrice parallela all'asse x e asse focale parallelo all'asse y.
Completando i quadrati
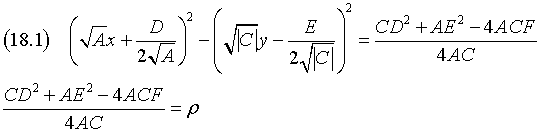
Se ρ non è positivo, l'iperbole non è reale. Altrimenti ha centro Ω e semiassi α e β
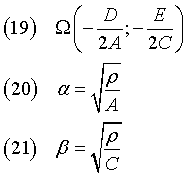
Le distanza φ dei fuochi dal centro Ω e l'eccentricità e sono
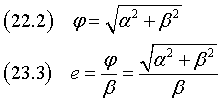
Le coordinate dei fuochi Φ1 e Φ2 sono
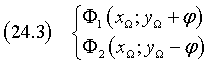
Detti P e Q i punti di intersezione della conica con l'asse focale (yP > yQ), H e K i punti di intersezione dell'asse focale con le direttrice (yH > yK), si ha
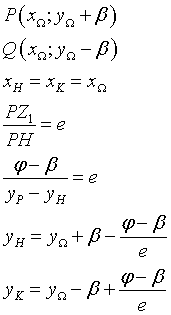
In definitiva, le equazioni delle direttrici sono
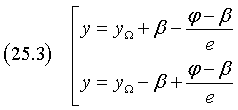
Se B ≠ 0, per la terza delle (2), a, b e e sono entrambi ≠ 0: direttrice e asse di simmetria sono obliqui rispetto ad entrambi gli assi cartesiani.
In questo caso, per calcolare le caratteristiche della conica, si ruota il sistema di riferimento cartesiano Oxy di un angolo θ in modo che l'equazione della conica nel sistema ruotato OXY abbia il coefficiente del monomio in XY uguale a 0, riportandosi a una delle situazioni esaminate nel paragrafo precedente.
Indicando con lettere maiuscole le coordinate nel sistema ruotato e con θ l'angolo di rotazione, le equazioni della rotazione R sono
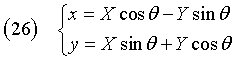
Dalla (1) si ha
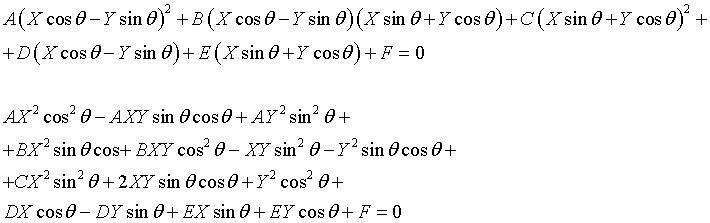
Riordinando in potenze decrescenti di X e Y
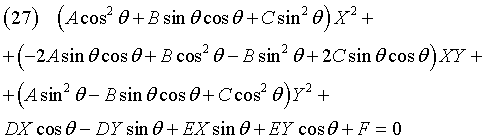
Il coefficiente di XY deve essere = 0:
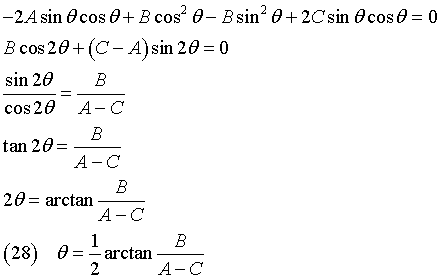
Dato l'angolo θ, si calcolano i coefficienti
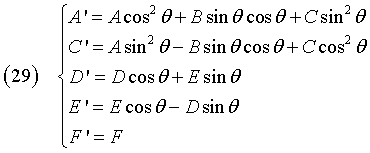
La (27) si riduce a
![]()
Per la (27.1) vale quindi l'analisi sviluppata nel paragrafo 3 per l'equazione (1) quando in essa B = 0 e A=A', C=C', D=D', E=E', F=F'.
Eccentricità e lunghezze di segmenti calcolate nel sistema OXY coincidono con le corrispondenti nel sistema Oxy, mentre le coordinate dei punti e le equazioni delle direttrici nel sistema Oxy vanno ottenute dalle corrispondenti nel sistema OXY sottoponendo queste ultime alla rotazione (26).
La seguente applicazione Javascript, dati i coefficienti A, B, C, D, E, F, calcola i parametri della conica e ne genera il grafico.
I coefficienti possono essere scritti come interi, reali in virgola fissa o come frazioni.
L'applicazione funziona appropriatamente solo se il vostro browser permette Javascript e le finestre popup.