Appunti per i Licei Scientifici
(a cura di Roberto Bigoni)
Dall'equazione canonica dell'ellisse è immediato dedurre le espressioni delle coordinate di un punto P dell'ellisse in funzione di una variabile comune rappresentata dall'angolo α che il vettore OP (dove O è l'origine del sistema canonico) forma con l'asse delle ascisse.
Infatti, posto
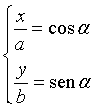
elevando al quadrato entrambi i membri e sommando membro a membro si ottiene l'equazione canonica
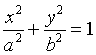
Esprimendo x e y in funzione di α
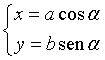
si ottengono le equazioni parametriche dell'ellisse.
Le equazioni parametriche di x e y si possono interpretare rispettivamente come ascissa e ordinata dei due punti A e B intercettati su due circonferenze centrate sull'origine O, una di raggio OA di misura a e l'altra di raggio OB di misura b, dalla semiretta uscente dall'origine O che forma un angolo α con l'asse delle ascisse.
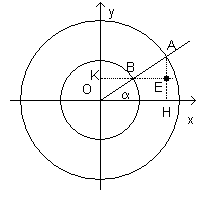
Il punto E della figura, che ha ascissa uguale a quella di A e ordinata uguale a quella di B, è un punto dell'ellisse di semiassi a e b.
Confrontando le ordinate yE e yA dei punti E e A della costruzione proposta, da
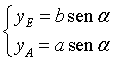
si ottiene
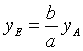
cioè l'ordinata di un punto E sull'ellisse di semiassi a e b è b/a dell'ordinata del punto A di uguale ascissa sulla circonferenza di centro coincidente con quello dell'ellisse e di raggio a.
Se, considerando per semplicità solo i punti di ordinata positiva, per ogni punto E e ogni punto A, si costruiscono rettangoli di base comune dx e altezze rispettive yE e yA, i primi rettangoli hanno area b/a di quella dei secondi.
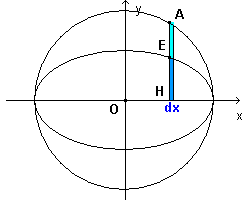
Di conseguenza la somma di tutti i primi rettangoli è b/a della somma di tutti i secondi. Ma per dx tendenzialmente nulli, la prima somma è l'area di mezza ellisse e la seconda somma è l'area di mezzo cerchio. In conclusione, l'area di mezza ellisse è b/a dell'area di mezzo cerchio e, ovviamente, l'area dell'ellisse è b/a di quella del cerchio.
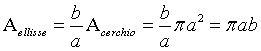
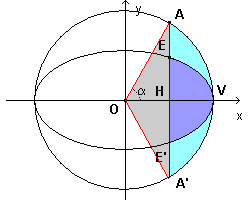
Una retta parallela all'asse delle ordinate di equazione
delimita la figura EE'V (colorata in viola nella figura) che viene denominata
segmento ellittico retto. L'area ε di questa figura risulta
b/a dell'area η del segmento circolare AA'V.
A sua volta l'area η può essere ottenuta sottraendo dall'area σ
del settore circolare AOA'V l'area τ del triangolo AOA'
L'area σ sta all'area del cerchio come il suo angolo al centro AOA' sta all'angolo giro, cioè come la sua metà α=AOV sta all'angolo piatto.
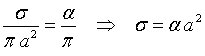
L'area τ risulta
Quindi l'area η è
e l'area ε è
Volendo esprimere quest'area in funzione di h si ha
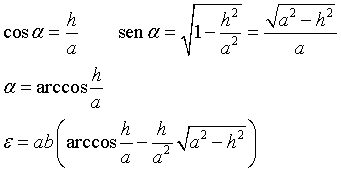
Esempio.
Data un'ellisse di semiassi a=4 e b=3, le aree dei segmenti ellittici che si ottengono tagliandola parallelamente all'asse minore ad una distanza h=2 dal centro misurano
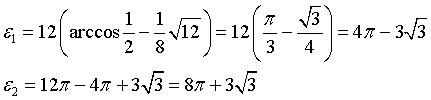
Si dimostra che il perimetro di un'ellisse di semiasse maggiore a e eccentricità e è
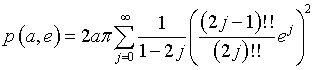
La seguente applicazione Javascript permette di approssimare il perimetro dell'ellisse.
ultima revisione: 19/09/2018