Tangenti ad una conica per un suo punto
(regola di sdoppiamento)

Appunti per i Licei Scientifici
(da Note Didattiche)

Una conica di eccentricità e e semilato retto l, nel sistema di riferimento cartesiano ortogonale XFY con origine in F, fuoco della conica, con asse delle ordinate parallelo alla sua direttrice e asse delle ascisse orientato dalla direttrice al fuoco, è descritta dall'equazione

equivalente a

Se i punti P(x_P;y_P) e Q(x_Q;y_Q) appartengono alla conica, dalla (1) si ha

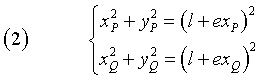
Sottraendo membro a membro nella (2) la prima equazione dalla seconda si ottiene

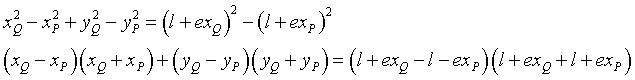
Semplificando

Il coefficiente angolare delle retta PQ è

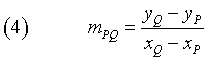
e quindi

Sostituendo questa espressione della differenza tra le ordinate nella (3) si ha

e, semplificando,

da cui

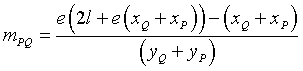
Il coefficiente angolare della tangente alla conica nel punto P è dato dal limite di m_PQ per Q→P:

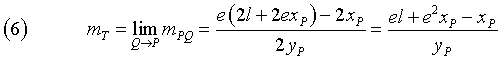
L'equazione della tangente alla conica in P si ottiene dall'equazione del fascio di rette per P assegnando al coefficiente angolare l'espressione (6)

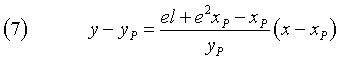
Si ottiene

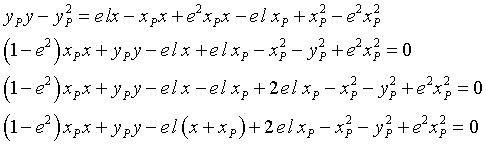
D'altra parte, dalla prime delle (2) si ha

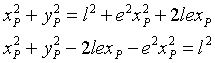
quindi l'equazione della tangente alla conica per P(x_P;y_P) è

Confrontando l'equazione (8) della tangente in P con l'equazione (1.1) della conica, si conclude che la (8) può essere dedotta immediatamente dalla (1.1)

• sostituendo al quadrato di ogni variabile il prodotto tra la variabile e la coordinata corrispondente del punto,
• e sostituendo ad ogni variabile la semisomma tra la variabile e la coordinata corrispondente del punto