Appunti per i Licei Scientifici
(da Note Didattiche)
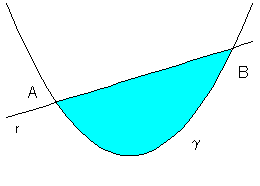
Dati in un piano una parabola γ e una retta r che interseca γ in due punti distinti A e B, la parte finita di piano delimitata dall'arco AB di γ e dal segmento AB di r è detta segmento parabolico.
In particolare, se la retta r è perpendicolare all'asse della parabola γ, il segmento parabolico si dice retto.
Per valutare l'area di un segmento parabolico retto si può operare nel seguente modo.
Si sceglie un sistema di riferimento con origine nel vertice di γ e asse delle ordinate coincidente con l'asse della parabola orientato dal vertice al fuoco. In tale sistema l'equazione di γ risulta
Detta B' la proiezione del punto B sull'asse delle ascisse e l la distanza OB', si suddivide OB' in n segmenti di ugual misura. Le ascisse degli estremi destri di questi segmenti risulteranno
Si costruiscono quindi i rettangoli aventi come base ognuno di questi segmenti e come altezza l'ordinata corrispondente al loro estremo destro calcolata sulla parabola.
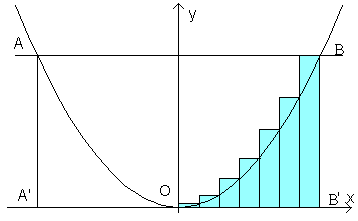
Il rettangolo di ordine i ha area
La somma R delle aree di tutti i rettangoli risulta
La differenza tra R e l'area S della figura delimitata dai segmenti OB' e B'B e dall'arco OB di γ risulta sempre positiva, ma diventa tanto minore quanto maggiore si prende il numero n di segmenti di OB'. Si esprime questa situazione dicendo che S è il limite di R per n che tende all'infinito e si può scrivere
Calcolando il valore della sommatoria, si ottiene quindi l'area S.
Per calcolare la somma dei quadrati dei primi n numeri naturali è utile costruire la seguente tabella
| i | i2 | Σ i2 | 6 Σ i2 | 6 Σ i2 |
|---|---|---|---|---|
| 1 | 1 | 1 | 6 | 1 · 2 · 3 |
| 2 | 4 | 5 | 30 | 2 · 3 · 5 |
| 3 | 9 | 14 | 84 | 3 · 4 · 7 |
| 4 | 16 | 30 | 180 | 4 · 5 · 9 |
| 5 | 25 | 55 | 330 | 5 · 6 · 11 |
Per induzione, si può concludere che
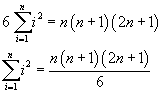
Utilizzando il risultato ottenuto, riprendendo l'espressione di R, si ha
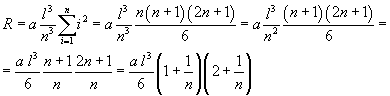
Per n infinitamente grandi, le frazioni di denominatore n si annullano e quindi
cioè l'area S è uguale a un terzo dell'area del rettangolo di base OB' e altezza B'B. Conseguentemente l'area della rimanente parte del rettangolo è due terzi dell'area dello stesso.
Per la simmetria della figura si può quindi concludere che l'area del segmento parabolico retto è due terzi dell'area del rettangolo circoscritto. Questa proprietà, dimostrata da Archimede di Siracusa, è nota come teorema di Archimede.
Se il segmento parabolico è generato dall'intersezione della parabola γ di equazione y=ax2 (a>0) con la retta r obliqua rispetto agli assi cartesiani, detti A e B i punti di intersezione e A' e B' le loro proiezioni sull'asse delle ascisse, l'area del segmento parabolico è ottenibile dalla differenza tra l'area del trapezio ABB'A' e la somma delle aree dei triangoli mistilinei S1 e S2.
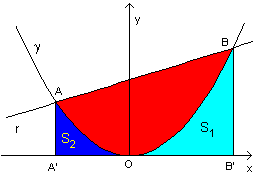
Dette xA e xB
(xA<0<xB) le ascisse di A e B, il segmento A'B'
ha misura
,
il segmento AA' ha misura
e il segmento BB' ha misura
.
L'area del trapezio ABB'A' è dunque
L'area del triangolo mistilineo S1 è un terzo di quella del rettangolo di lati OB' e BB' e l'area del triangolo mistilineo S2 è un terzo di quella del rettangolo di lati OA' e AA', cioè
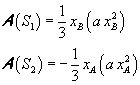
L'area del segmento parabolico AOB risulta dunque
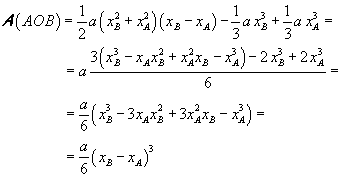
Questa espressione dell'area del segmento parabolico vale in generale per ogni parabola
di equazione
con a>0.
Infatti, traslando l'origine del sistema di riferimento nel vertice della parabola si
riproduce la configurazione studiata.
Ovviamente, se a è negativo, va considerato in valore assoluto.
In definitiva, data una parabola di equazione
intersecata da una retta nei punti di ascisse rispettivamente
xA e xB (xA<xB),
il segmento parabolico così determinato ha area
ultimo aggiornamento: 03/06/2016