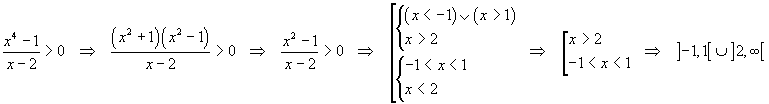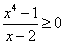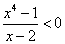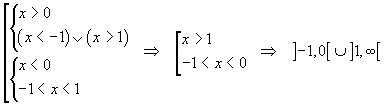Frazioni algebriche
Le frazioni algebriche, cioè le funzioni definite dal rapporto tra due polinomi, non esistono negli zeri del denominatore
e sono positive solo negli intervalli in cui numeratore e denominatore sono concordi.
Operativamente, definito il dominio di esistenza, conviene condurre lo studio del segno della frazioni algebriche
con un metodo analogo a quello indicato per i polinomi:
- si scompongono numeratore e denominatore in prodotti di potenze dai fattori di primo o secondo grado;
- si trascurano i fattori di segno costantemente positivo;
- si studia il segno dei fattori variabili (binomi e trinomi);
- si individuano gli intervalli in cui il numero dei fattori negativi è nullo o pari.
Esempi.
-
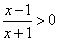
Questo problema è assomiglia a quello dello studio del segno del trinomio
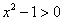 con esclusione del valore -1 che annulla il denominatore.
con esclusione del valore -1 che annulla il denominatore.
L'unico zero si ha in 1. Il dominio di positività è ]-∞,-1[U]1,∞[
-
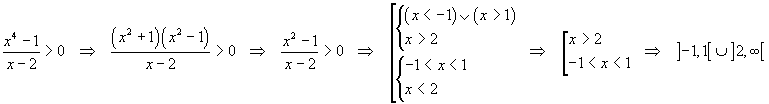
-
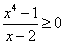
vanno uniti alla soluzione del caso precedente anche gli zeri del numeratore: [-1,1]U]2,∞[
-
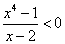
la soluzione è l'insieme complementare (nel dominio di esistenza) della precedente soluzione: ]-∞,-1[U]1,2[
-
La disequazione 2 con Wolframalpha:
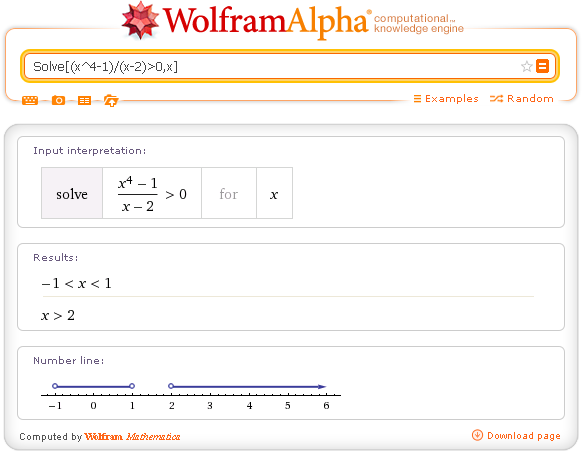
Nel caso in cui la funzione da analizzare sia rappresentata dalla somma di due o più frazioni, eseguendo la somma
ci si riporta ai casi precedenti.
La disequazione 6 con Wolframalpha:
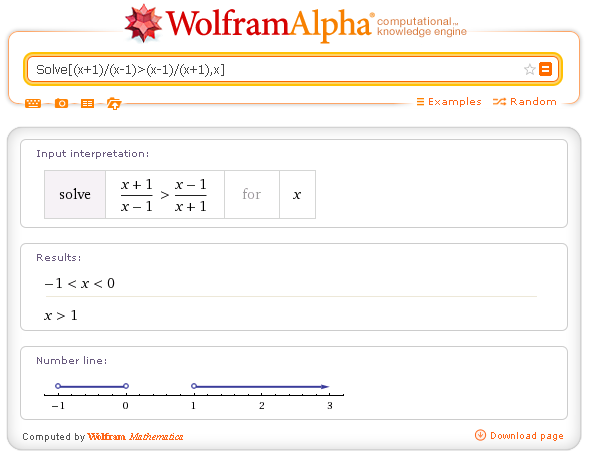
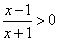
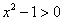 con esclusione del valore -1 che annulla il denominatore.
con esclusione del valore -1 che annulla il denominatore.