Funzioni irrazionali

Si dicono funzioni irrazionali le funzioni espresse da radicali.

Va osservato che, nel campo dei reali, una radice con indice intero dispari n

non è strettamente equivalente ad una esponenziale

Infatti la (1) è reale per ogni x, mentre la (2) è reale solo per x>0.

Questa differenza tra le due funzioni può creare confusioni. Ad esempio, la radice cubica reale di -1 è -1, perché (-1)³=-1.

Ma se si prova a calcolare la radice cubica di -1 con la calcolatrice di Windows scrivendo -1, settando Inv e cliccando il tasto x³, la calcolatrice dice valore non valido. La stessa cosa succede se si usa il tasto x^y con x negativo e y non intero.

Evidentemente la calcolatrice usa un algoritmo che assimila i radicali a potenze con esponente frazionario, possibili solo se la base è non negativa.

Dato che una funzione per definizione deve essere univoca, i radicali si intendono radicali univoci, cioè aritmetici.

Questo è comunque vero se l'indice del radicale è dispari (radice dispari): in questo caso non ci sono problemi di realtà e il segno del radicale coincide con il segno del radicando.

Radicali di indice dispari.

I confronti tra un radicale di indice dispari e un numero si risolvono elevando entrambi i membri alla potenza uguale all’indice del radicando.

Esempio

Stessa procedura si applica nel confronto tra un radicale dispari e una funzione razionale

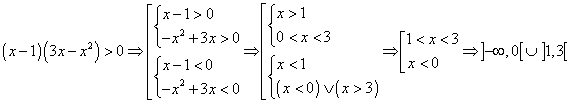
figura 4

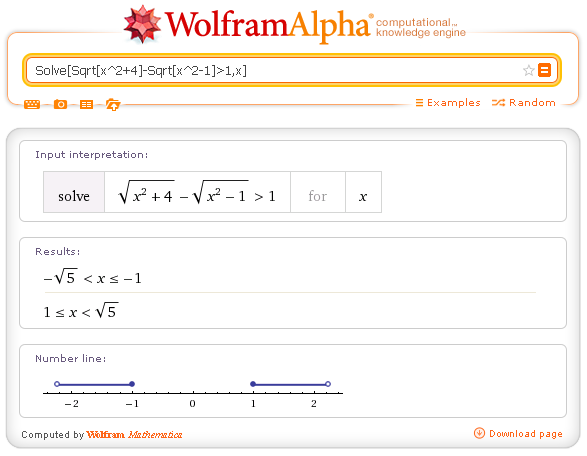
Soluzione della disequazione con WolframAlpha

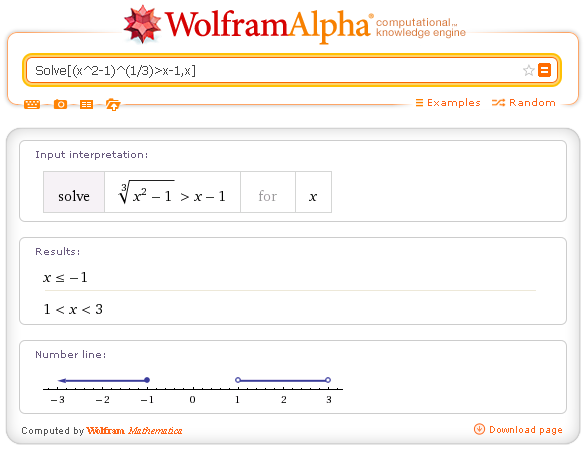
WolframAlpha (cioè Mathematica) ammette solo soluzioni negative ≤-1; la discrepanza rispetto alla soluzione mostrata su sfondo blu è dovuta al fatto che, evidentemente, Mathematica assimila la radice cubica ad una esponenziale con esponente frazionario (e in effetti come tale è stata scritta nel campo di input), ma le esponenziali sono reali solo se la base non è negativa.

Confronto tra un radicale di indice pari e un numero.

Se l'indice è pari (radice pari), la funzione è reale solo dove il radicando è non negativo (≥0).
Una radice pari, nel suo dominio di realtà, è sempre non negativa.

Il confronto di una radice pari con un numero negativo è immediato

Nel confronto di maggioranza di un radicale pari con un numero positivo si possono direttamente elevare a potenza entrambi i membri, perché questa operazione implica, per assorbimento, la condizione di realtà del radicale.

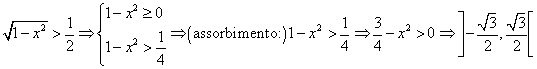
figura 8

Confronto tra un radicale di indice pari e una funzione razionale.

Maggioranza

Nel confronto di maggioranza di una radice pari con una funzione razionale (polinomio o frazione)

si distinguono le due eventualità:

se r(x) è negativa, la radice, nel suo campo di esistenza, è non negativa, quindi maggiore di r(x);
se r(x) è non negativa, f(x) deve essere maggiore del quadrato di r(x) (questa condizione assorbe la condizione di realtà, che quindi è superflua)

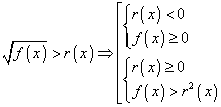
figura 10

Esempio:

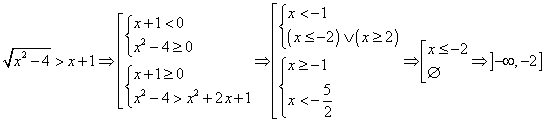
figura 11

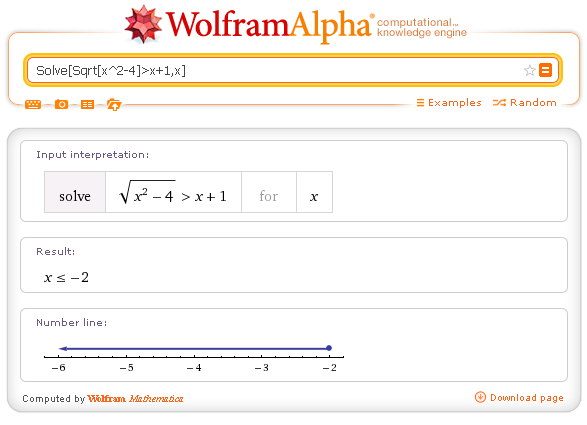
Soluzione della disequazione con WolframAlpha

Minoranza

Per risolvere il confronto

sarà sufficiente intersecare il complementare dell’insieme trovato nel caso precedente con il dominio di realtà del radicale.

Nell’esempio proposto si ottiene

Il confronto

ha come soluzione quella di

senza i valori che uguagliano le funzioni.

Nell'esempio proposto

cioè lo stesso insieme tra trovato, perché non esistono soluzioni all'equazione

La soluzione del confronto

può comunque essere determinata direttamente

imponendo la realtà del radicale;
imponendo la positività della funzione razionale (se non fosse positiva, non potrebbe essere maggiore di una funzione che, dove è reale, è non negativa);
elevando al quadrato entrambi i membri.

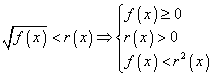
figura 19

Riprendendo l'esempio già trattato

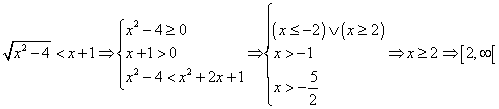
figura 20

Quando un confronto coinvolge più radicali pari, prima di tutto bisogna imporre le condizioni di realtà dei singoli radicali, quindi cercare di razionalizzare il confronto con opportuni elevamenti al quadrato di entrambi i termini del confronto. Va fatta attenzione al fatto che l'elevamento al quadrato di entrambi i termini produce un confronto equivalente solo se entrambi i termini sono non negativi.

Esempio:

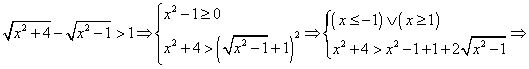
figura 21

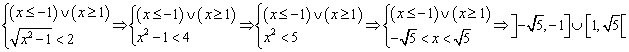
figura 22

Soluzione della disequazione con WolframAlpha