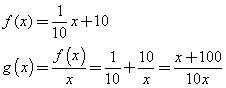
Le funzioni f(x) e g(x) sono
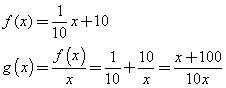
Ovviamente le due funzioni hanno senso applicativo solo per x>0.
f(x) è l'equazione di una retta di coefficiente angolare 1/10 e intercetta 10.
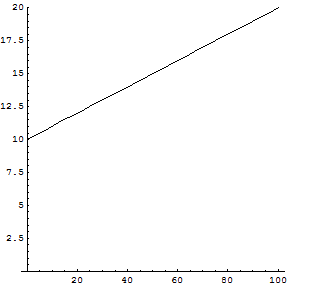
g(x) è una funzione omografica il cui grafico è un'iperbole equilatera traslata con asintoti
paralleli agli assi cartesiani
e
per cui non ha né massimi né minimi.
La funzione f(x) rappresenta semplicemente il fatto che, se non si fanno telefonate, si pagano comunque 10€ al mese e che il costo mensile aumenta proporzionalmente ai minuti di utilizzo.
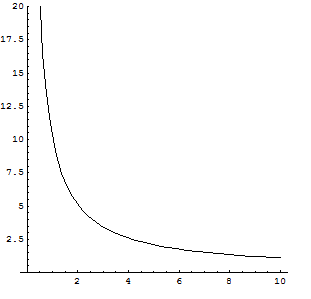
La funzione g(x) esprime il fatto che il calcolo del costo medio al minuto non ha senso se non si fanno telefonate e che l'incidenza del costo fisso sul costo di una minuto cala in modo inversamente proporzionale al numero dei minuti di conversazione.
Si ha
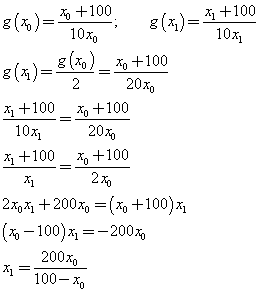
Anche questa è una funzione omografica con asintoto orizzontale
e asintoto verticale
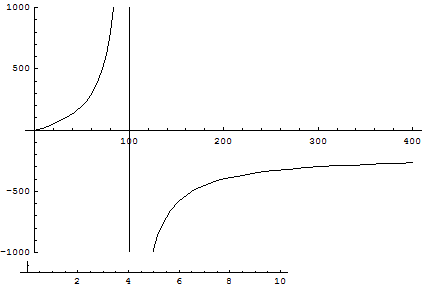
L'asintoto verticale indica quanto dovrebbe durare una telefonata per dimezzare il costo medio attuale.
La funzione polinomiale richiesta è quella di una parabola di equazione
Le coordinate dei punti devono soddisfare questa equazione.
Per il punto A si ottiene immediatamente c = 2. Quindi
Per i punti B e C si ottiene
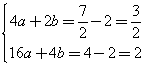
Si ottiene
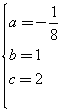
quindi
L'area sottesa dall'arco di parabola disegnato è data dall'integrale
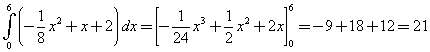
L'area di "Z" è 1/2, quindi l'area coperta è
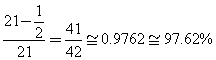
L'area coperta è leggermente superiore a quella indicata.
Con le nuove tariffe, per x>500 si ha
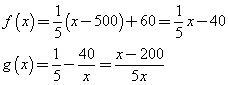
Per x tendente a 500 da sinistra e da destra le due funzioni tendono tendono agli stessi valori, rispettivamente 60 e 3/25, per cui sono entrambe continue, ma non sono derivabili: la f(x) perché le rette che la rappresentano a sinistra e a destra di 500 hanno diverso coefficiente angolare; la g(x) perché le sue derivate a sinistra e a destra di 500 sono rispettivamente
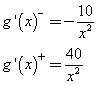
f(x) è sempre crescente perché le rette che la rappresentano hanno entrambe coefficienti angolari positivi.
g(x) è negativa a sinistra di 500 e positiva a destra, per cui si ha un minimo assoluto per x=500. Per questo valore il costo medio per minuto ha un minimo di 0.12€.