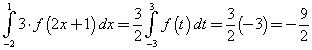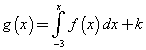
Il grafico presenta tre punti con tangente orizzontale, cioè tre punti distinti in cui la derivata dell'eventuale polinomio si annulla. Quindi la derivata deve essere almeno di terzo grado e il polinomio almeno di quarto grado.
Rappresentando g(x) come
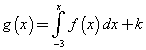
sommando le aree, assumendo negative quelle al di sotto dell'asse x, si ha
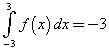
quindi
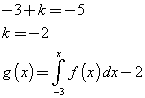
g(x) è decrescente da -3 a -2, crescente da -2 a 0, poi sempre non crescente. Presenta quindi un massimo assoluto per x = 0.
La derivata prima di g(x) è f(x) e la sua derivata seconda è data dal coefficiente angolare della tangente a f(x) che risulta positivo da -3 a -1 e da 1 a 2. Dunque la concavità di g(x) è positiva in ]-3,-1[ e in ]1,2[.
Si ha
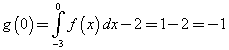
Per x=0 il numeratore e il denominatore della frazione
si annullano. Per calcolare il limite della frazione per x→0 si può applicare il teorema di
de l'Hôpital:
Ponendo
si ha
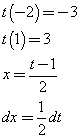
Quindi
