Il coefficiente angolare della tangente coincide con il valore della derivata prima. Quindi
Nel secondo quadrante si ha x = -2 e y(-2) = 9 e qundi f(2) = 9. L'espressione di f(x) è data da
quindi
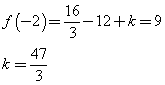
In definitiva
Il volume del tronco di cono si può determinare applicando il teorema di Guldino alla rotazione di un trapezio rettangolo di basi R e r e lato retto h attorno al lato retto.
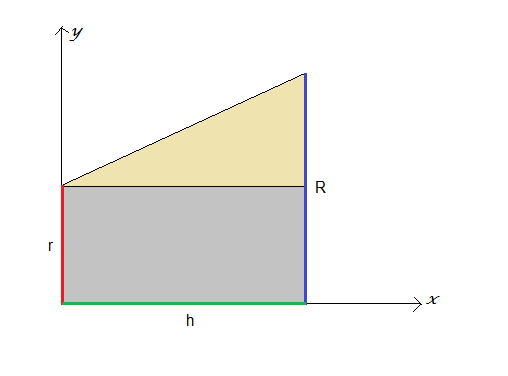
Il trapezio può essere scomposto in un rettangolo di lati h e r e in un triangolo rettangolo di cateti h e R-r.
La rotazione del rettangolo attorno al lato h è un cilindro di volume
L'area del triangolo rettangolo è 
.
Il baricentro del triangolo ha ordinata 
.
Per il teorema di Guldino il volume di rotazione del triangolo è
.
L'area del tronco di cono si ottiene sommando V1 e V2
La probabilità che venga testa al più due volte è la somma della probabilità che non venga mai testa, che venga una sola volta o che venga due volte. Le tre probabilità sono rispettivamente
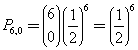
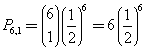
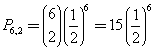
In totale 
La seconda probabilità richiesta si ottiene sottraendo da 1 la probabilità che non venga mai testa e la probabilità che venga una sola volta:
Le derivate di y(x) sono
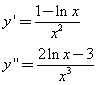
Osservando che nella quarta delle equazioni proposte tutti gli addendi hanno denominatore x, questa appare la risposta più probabile. In effetti sostituendo in essa le espressioni della y e delle sue derivate, l'uguaglianza risulta verificata.
La retta chiesta coincide con il vettore direttore del piano applicato all'origine.
Le equazioni parametriche della retta sono
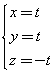
da cui
La derivata prima di f(x) è
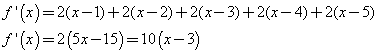
f'(x) è positiva per x > 3, negativa per x < 3 e nulla per x = 3. Dunque la funzione ha un minimo per x = 3 che vale
L'area di un poligono regolare di n lati inscritto in una circonferenza di raggio r è data dalla
somma delle aree di n triangoli isosceli uguali di lato r e angolo al vertice
. Ogni area vale
quindi l'area del poligono è
Posto 
, si ha
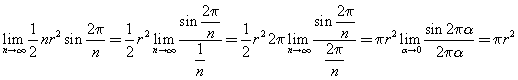
Detta A l'area del triangolo, la probabilità richiesta è si ottiene sottraendo da A le aree dei settori circolari di raggio r = 2 con centri sui vertici e calcolando il rapporto tra questa differenza e A.
A può essere calcolata in vari modi, ad esempio con il teorema di Erone:
dove
p è il semiperimetro e a, b, c sono le misure dei lati. Quindi
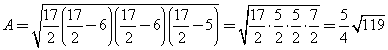
Dato che la somma degli angoli interni di un triangolo è π, la somma delle aree dei settori circolari
equivale ad una semicirconferenza di raggio r = 2, quindi vale
. La probabilità è dunque
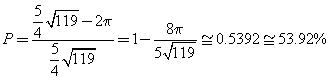
Perché si possa applicare il teorema di Lagrange, la funzione deve essere continua e derivabile in tutti i punti interni dell'intervallo considerato. In particolare per x = 1, il limite da sinistra della funzione vale 1 e deve coincidere con il limite da destra che vale
La funzione è continua in 1 per ogni k.
La derivata sinistra è 3x2 e per x→1 tende a 3. La derivata destra è 2x-k e per x→1 tende a 2-k. Perché la funzione sia derivabile in 1 bisogna che
Quindi a destra di 1 la funzione è espressa da
Il teorema di Lagrange afferma che deve esistere almeno un punto interno all'intervallo in cui il valore della derivata è
Se il punto cercato è a sinistra di 1, si ha
Risulta ammissibile solo la radice positiva. Se il punto è a destra di 1 si ha
Questa soluzione non è accettabile perché minore di 1.
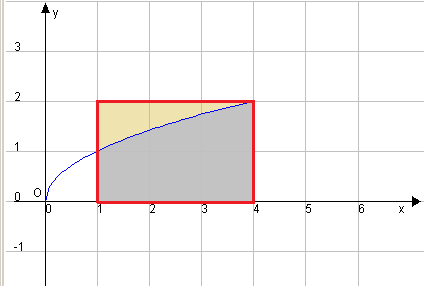
Il grafico della funzione è un arco di parabola con vertice nell'origine, asse di simmetria coincidente con l'asse x.
Per il teorema di Archimede l'area sottesa dall'arco diparabola nell'intervallo [0,4] è 2/3 dell'area del rettangolo circoscritto,
cioè 16/3. L'area sottesa dallo stesso arco nell'intervallo [1,4] si ottiene sottraendo dalla precedente l'area sottesa dall'arco
nell'intervallo [0,1], cioè 2/3. Quindi l'area sottesa dall'arco nel'intervallo [1,4] è 14/3. La porzione rimanente
del rettangolo è 
Il rapporto tra le due aree è 2/7.