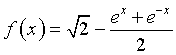
La funzione
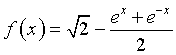
può essere più semplicemente scritta come
Il coseno iperbolico è una funzione pari definita su tutto R, decrescente per x negative, crescente per x positive con un minimo in (0;1). La funzione f, differenza tra una costante positiva e un coseno iperbolico, è pure pari, ma crescente per x negative e decrescente per x positive con un massimo M in (0; √2-1), corrispondente al valore graficato.
Il valore di a si ottiene risolvendo l'equazione
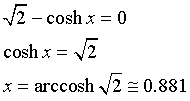
Si ricorda che la differenza tra i quadrati del coseno iperbolico e del seno iperbolico è 1 e che la derivata del coseno iperbolico è il seno iperbolico e viceversa.
Si ha
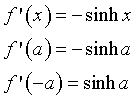
La derivata destra per x=a della funzione graficata in figura 3 è uguale a f'(-a).
Le derivate coincidono con i coefficienti angolari m e m' delle tangenti in A(a,0). Si ha
Quindi le tangenti a destra e a sinistra sono perpendicolari.
Il lato della ruota ha misura 2. La lunghezza dell'arco di estremi in (-a;0) e (a;0) è
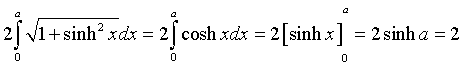
Con riferimento alla figura 4 del testo, la tangente trigonometrica dell'angolo LAM è 
e, per la similitudine dei triangoli LAM e ALC, t è anche la tangente trigonometrica dell'angolo LCA, quindi il cateto
AL del triangolo ALC, dato che il cateto CL misura 1, ha misura coincidente con t. L'ipotenusa AC dello stesso triangolo è
In definitiva, l'ordinata d di C è
cioè è costante.
Con considerazioni analoghe a quelle svolte per la precedente funzione f, la nuova funzione f è esprimibile come
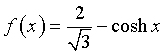
Il grafico di questa funzione ha un andamento analogo a quello della precedente con un massimo in
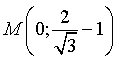e che interseca l'asse delle ascisse nei punti di ascissa
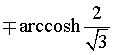. È facile verificare che questi valori coincidono con quelli espressi da logaritmi nel testo.
In questo caso i valori dei coefficienti angolari delle tangenti sinistra e destra nei punti angolosi risultano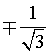 
.
Gli angoli che tali tangenti formano con l'asse delle ascisse sono di 30° e 150°; tra loro formano un angolo di 120°. Il poligono regolare con angoli nei vertici di 120° è l'esagono.