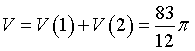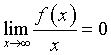perché il numeratore è limitato mentre il denominatore diverge.La funzione è continua in tutti i punti del grafico in cui esso non subisce interruzioni e è derivabile in tutti i punti in cui è continua e nei quali è possibile determinare la tangente in modo univoco. Quindi la funzione descritta dal grafico proposto è continua su tutto R e non è derivabile per x = (2n+1) con n∈N.
Il limite della funzione per x→∞ non esiste in quanto la funzione è chiaramente oscillante.
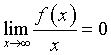perché il numeratore è limitato mentre il denominatore diverge.
La derivata prima g(x) da 0 a 1 ha valore costante 1; in 1 non esiste; da 1 a 3 ha valore costante -1; in 3 non esiste; da 3 a 4 ha valore costante 1.
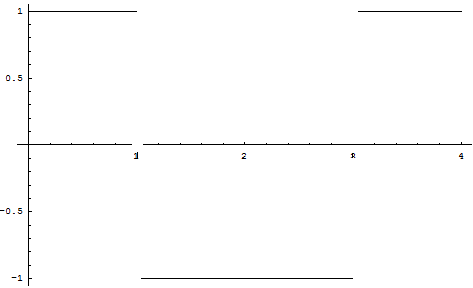
La funzione integrale h(x) ha andamento parabolico crescente da 0 a 1, dove raggiunge il valore 1/2; ha ancora andamento parabolico nell'intervallo [1;3], crescente da 1 a 2, decrescente da 2 a 3; è ancora crescente da 1 a 2; per x = 2 ha un massimo uguale a 1; nel resto dell'intervallo la funzione ha andamento parabolico decrescente fino a tornare al valore 0.
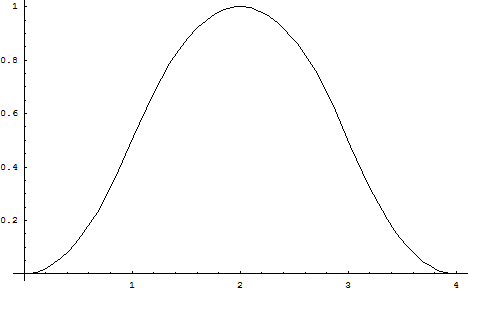
La funzione s ha periodo uguale a quello della funzione f, cioè 4, se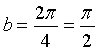 
.
Infatti i punti O, B, D, E della figura 1 del testo appartengono anche al grafico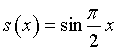 
.
Nell'intervallo [0;1] i grafici individuano le seguenti zone
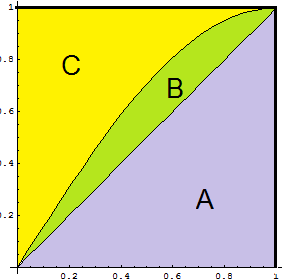
Le probabilità richieste sono date direttamente dalle loro aree.
L'area della zona A è 1/2.
L'area sottesa dall'arco di sinusoide è
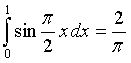
L'area della zona B è quindi
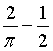
e l'area della zona C è
Poiché i quadrati dei numeri minori di 1 sono minori della base, si può subito dire che l'area A diminuisce e l'area C aumenta.
Per l'area B le considerazioni qualitative sono insufficienti quindi è necessario un calcolo esplicito.
Il nuovo valore dell'area A è
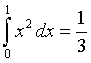
con variazione negativa
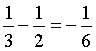
L'area sottesa da s2 è
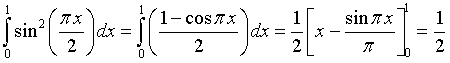
Il nuovo valore dell'area B è quindi
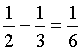
con variazione positiva
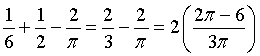
La nuova area della zona C è
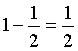
con variazione positiva
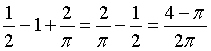
Integrando l'equazione della retta OB con la condizione che h(0) = 0, si ottiene l'espressione analitica della funzione h nell'intervallo [0;1]:
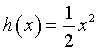
Il solido generato dalla rotazione dell'arco del grafico di h attorno all'asse delle y può essere calcolato come somma dei volumi di strati cilindrici di raggio x, spessore infinitesimale dx e altezza h(x) e raggio
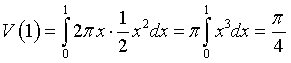
Integrando l'equazione della retta BD con la condizione che h(2) = 1, si ottiene l'espressione analitica della funzione h nell'intervallo [1;3]:
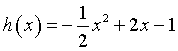
Si ha quindi
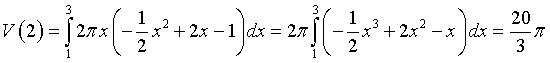
e infine
