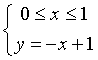
La funzione f(x) dell'esempio è un segmento di retta di coefficiente angolare m=-1 e intercetta q=1. La sua descrizione analitica è
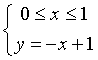
Per i quattro lati del quadrato Λ si osserva che
![]()
Infatti, se x≥0 & y≥0 (1° quadrante)
![]()
se x<0 & y≥0 (2° quadrante)
![]()
se x<0 & y<0 (3° quadrante)
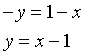
se x≥0 & y<0 (4° quadrante)
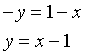
Quindi una sintetica descrizione analitica di Λ è
![]()
Se f(x) è di 2°
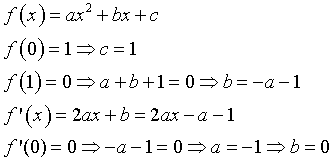
Si ottiene
![]()
Per il teorema di Archimede, l'area del primo quadrante sottesa dall'arco di parabola è 2/3 dell'area del quadrato circoscritto, cioè circa il 67%, quindi questa funzione non è accettabile.
Provando un polinomio di 3°
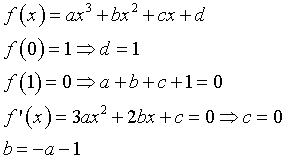
Si ottiene
![]()
Si impone che l'area sottesa dal grafico della curva tra 0 e 1 sia 0.55
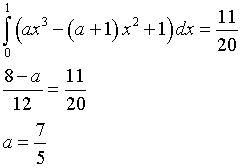
L'equazione della cubica è quindi
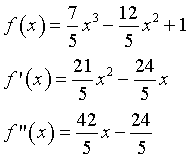
La cubica presenta una simmetria centrale rispetto ad un punto di flesso F, la cui ascissa si ricava azzerando la derivata seconda
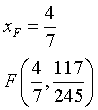
Al massimo in (0,1) corrisponde un minimo simmetrico rispetto a F.
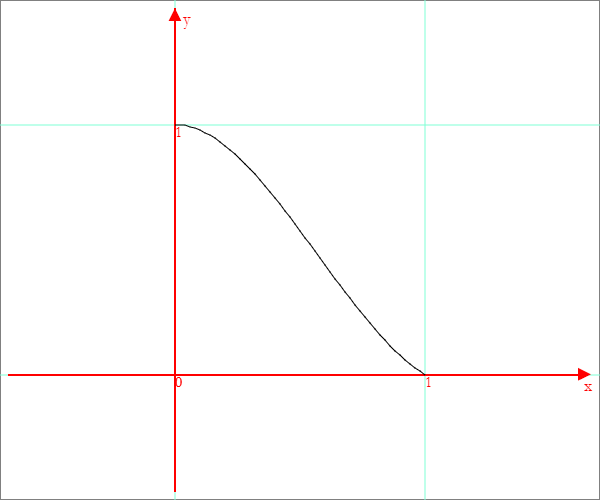
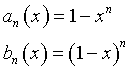
Le condizioni sui valori agli estremi dell'intervallo I = [0,1] sono di verifica immediata.
Nell'intervallo J=]0,1[
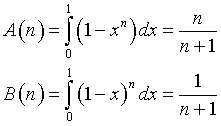
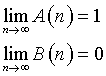
All'aumentare di n l'area sottesa dal grafico di an tende a coincidere con il quadrato.
All'aumentare di n l'area sottesa dal grafico di bn tende ad annullarsi.
Il disegno derivato da a2(x) è descritto dall'equazione ![]()
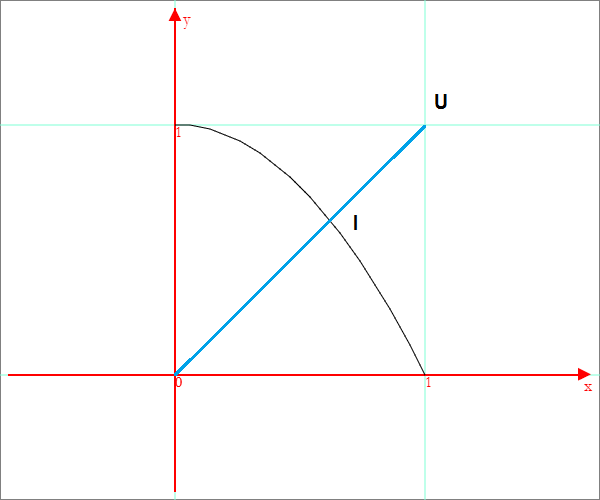
Il punto I di intersezione della curva con la diagonale si ottiene risolvendo per coordinate positive il sistema
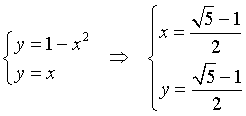
La distanza dell'intersezione dal punto U(1,1) è
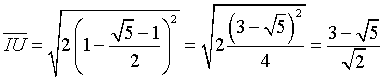
La probabilità che la goccia cada nell'intervallo IU nel 20% dei casi è
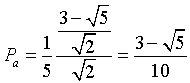
Il numero di mattonelle difettose di questo tipo è
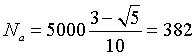
Il disegno derivato da b2(x) è descritto dall'equazione ![]()
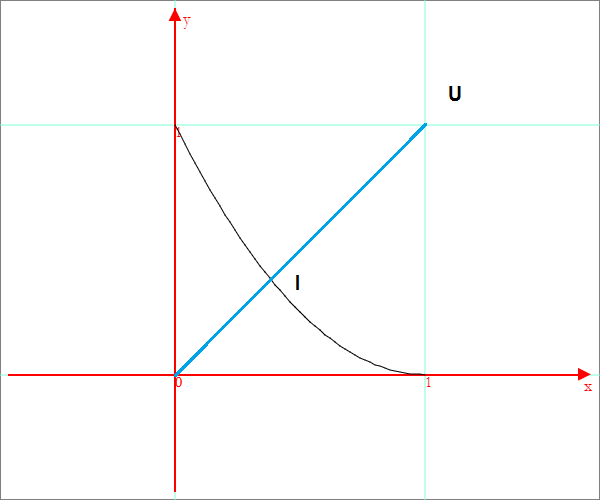
Il punto I di intersezione della curva con la diagonale si ottiene risolvendo il seguente sistema e scegliendo l'intersezione più vicina all'origine
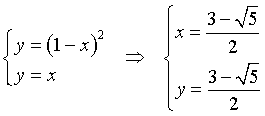
La distanza dell'intersezione dal punto U(1,1) è
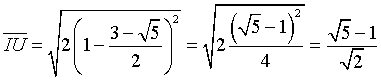
La probabilità che la goccia cada nell'intervallo IU nel 20% dei casi è
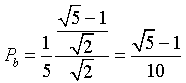
Il numero di mattonelle difettose di questo tipo è
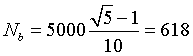
In definitiva il numero delle mattonelle difettose è 1000.