![]()
Detti P e Q i punti di tangenza, si ha
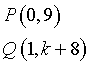
Inoltre
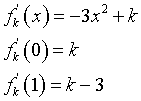
Le rette tangenti hanno equazioni
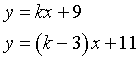
Mettendole a sistema si ottiene x=2/3.
L'ordinata di M, ricavabile immediatamente dalla prima delle due equazioni precedenti, è
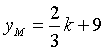
Risolvendo la disequazione
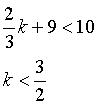
risulta che il massimo intero positivo richiesto è 1.
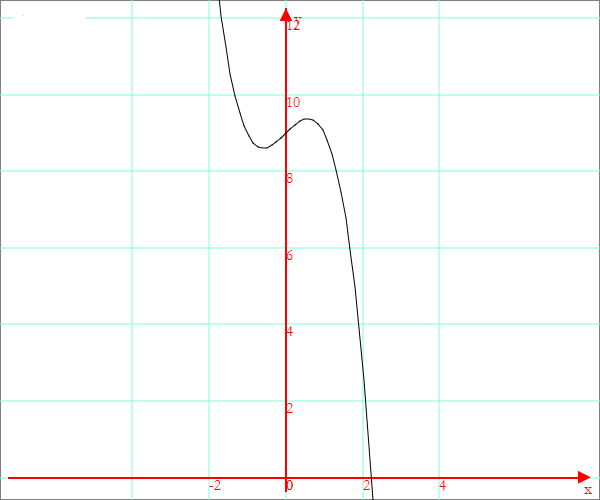
La funzione da studiare è
![]()
Si tratta di una funzione polinomia di terzo grado reale e continua per ogni x∈ℜ. Il suo grafico è una cubica, curva caratterizzata dalla simmetria centrale rispetto a un punto di flesso e dalla presenza di due punti simmetrici di massimo e minimo locali. Per x→+∞ la funzione tende a -∞ e per x→-∞ la funzione tende a +∞.
Il punto di flesso si individua azzerando la derivata seconda.
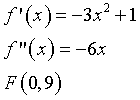
Gli estremanti si individuano azzerando la derivata prima.
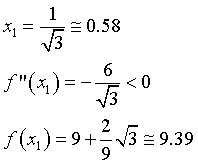
La funzione presenta un massimo
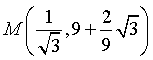
e un minimo N, simmetrico di M rispetto a F.
Le rette r1 e s1 hanno equazioni
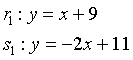
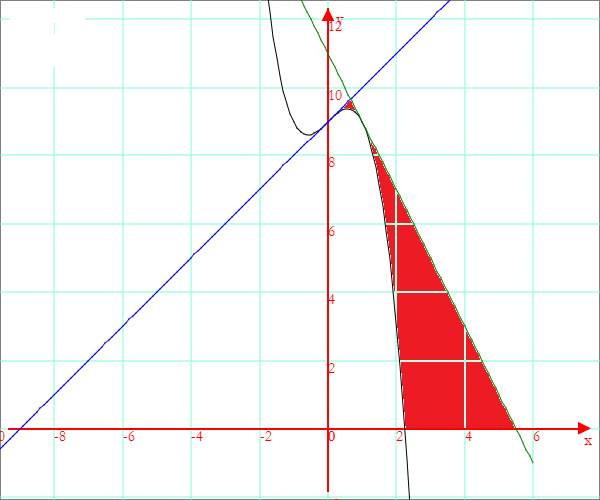
I vertici del triangolo T sono
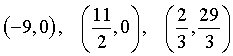
e la sua area è
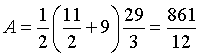
La regione dei punti P è rappresentata dalla zona colorata in rosso nella figura. L'area di questa regione si può ottenere sottraendo da A l'area B della parte di triangolo compresa nel 2° quadrante e poi sottraendo dalla differenza A-B l'area sottesa dall'arco di Γ1 da 0 allo zero z di Γ1.
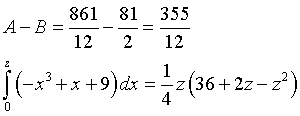
Poiché f(2.24)=0.000576, 2.24 può essere una sufficiente approssimazione di z, quindi
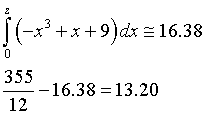
La probabilità richiesta è quindi circa
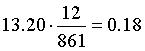
Il coefficiente angolare m(t) della normale è l'opposto del reciproco della derivata prima
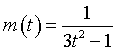
L'equazione di tale perpendicolare per il punto N(t,-t3+t+9) è
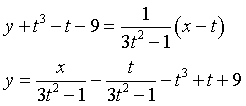
Perchè la retta passi per l'origine bisogna che
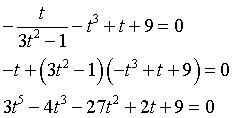
Le soluzione di questa equazione possono essere rappresentate dalle intersezioni delle curve di equazioni
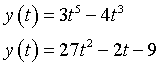
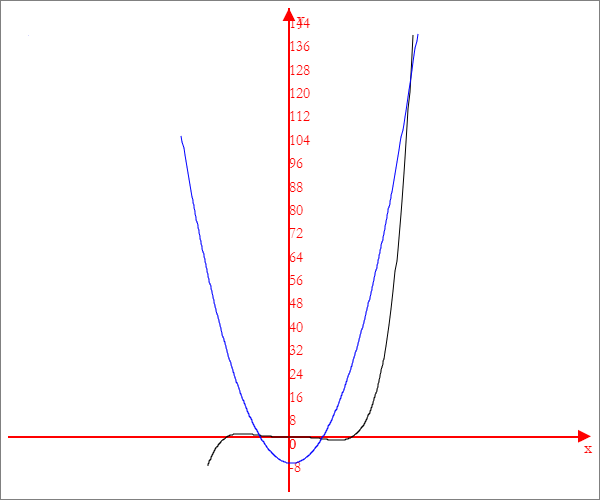
In generale se P(x) è un polinomio di grado n, l'equazione della normale al grafico di P(x) nel punto N(t,P(t)) è
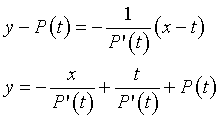
Il passaggio della retta per l'origine impone
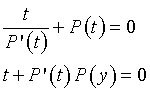
Questa è un'equazione polinomiale di grado 2n-1 che ammette al massimo 2n-1 soluzioni reali.