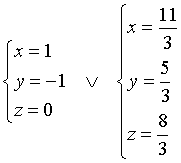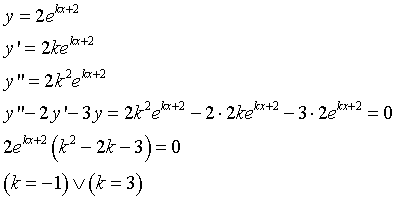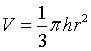
Supponendo che il cono sia retto, siano r il raggio della sua base e h la sua altezza. Il volume del cono è quindi
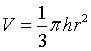
Indicando con x l'altezza del cilindro inscritto (0<x<h) e con y il raggio della sua base, si ha
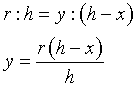
Il volume U(x) del cilindro è
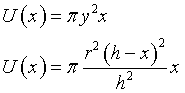
Bisogna dimostrare che 2U(x) < V.
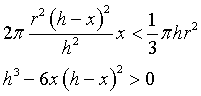
cioè che il massimo di f(x)=6x(h-x)2 è minore di h3. Questo massimo si ha per x = h/3 e vale 8/9h3.
Detta pi la probabilità che esca i, posto p4 = x, si ha
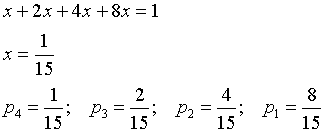
La probabilità richiesta è
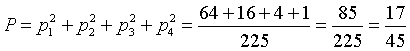
Perché le due curve siano tangenti bisogna che le loro derivate coincidano.
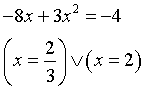
Bisogna inoltre che coincidano i loro valori.
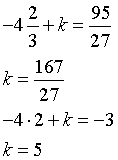
Per x→+∞ il numeratore diverge positivamente dato che il sottraendo esponenziale è comunque finito. L'esponenziale a denominatore converge a 0 e il coseno oscilla tra -1 e +1, per cui il denominatore e comunque finito. In conclusione la funzione diverge positivamente.
Per x→-∞ il numeratore diverge negativamente mentre il denominatore diverge positivamente. Ma l'infinito del denominatore è di ordine maggiore di quello del numeratore, per cui la funzione tende a 0.
Detta x la misura della metà del lato lungo del rettangolo e y la misura dell'altro lato, il perimetro p della figura è
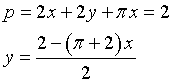
L'area a(x) della figura è quindi
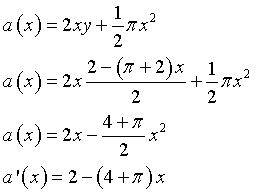
a'(x) si annulla per
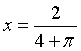
quindi le misure dei lati sono
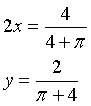
Detto C il centro della circonferenza, le componenti del vettore CT sono
![]()
Questo vettore deve essere perpendicolare al piano π; le sue componenti devono essere proporzionali ai coefficienti 3, -1, -2.
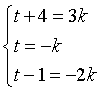
Si ottiene k=1 e t=-1, quindi le coordinate di C sono
![]()
La lunghezza del vettore CT è √14 e l'equazione della circonferenza
![]()
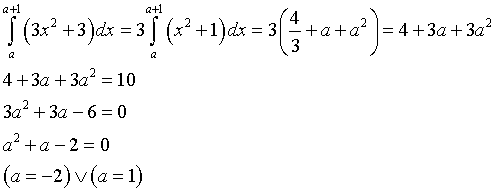
La probabilità Pn,k che un giocatore vinca k volte in n prove è
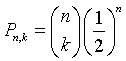
La probabilità che in 12 partite il primo giocatore ne vinca almeno 10 è
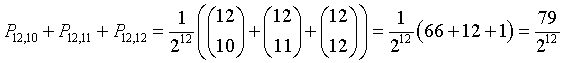
La probabilità analoga per il secondo giocatore è identica alla precedente, per cui la probabilità richiesta è
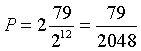
È immediato verificare che le coordinate dei tre punti soddisfano l'equazione del piano e che le loro distanze reciproche sono tutte uguali a √8. Quindi il triangolo è equilatero.
Anche le distanze di P(x,y,z) dai tre punti devono essere uguali a √8.
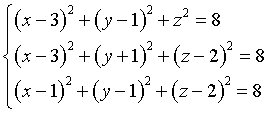
Con opportune riduzioni si ottiene un sistema di secondo grado che ammette soluzioni