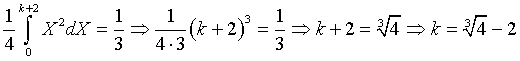.L'arco di parabola Γ1 passa per il punto (0;1) solo se a=1/4. L'arco di circonferenza Γ2 passa per il punto (0;1) solo se b=-1. L'arco di iperbole Γ3 passa per il punto (1;0) solo se c=-1.
Dal grafico si deduce agevolmente che la f è derivabile a destra per x=-2 in cui la tangente destra è l'asse delle ascisse; per x=0 le derivate sinistra e destra sono diverse: si ha un punto angoloso e non esiste tangente; per x=1 si ha una cuspide e la tangente è la retta di equazione x=1.
L'equazione di Γ1 è .
L'equazione di Γ2 è 
.
L'equazione di Γ3 è
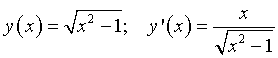
con
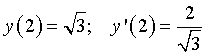
Per x=2 l'equazione della tangente è
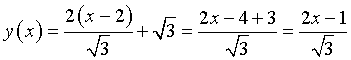
Per Γ1 la derivata è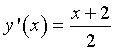 
.
Per Γ2 la derivata è 
.
Il grafico della derivata è
La derivata della funzione F(x) è ovviamente la funzione f(x) e la derivata seconda di F(x) è f'(x) quindi la concavità di F(x) è data dal segno di f'(x): F(x) è convessa per x<0 e x>1, concava per 0<x<1.
La funzione nel dominio indicato è un arco di parabola.
Questa funzione nel suo dominio è sempre crescente, quindi è biunivoca e quindi invertibile. Esprimendo x in funzione di y si ha
Per ottenere l'equazione della funzione inversa si scambiano le variabili, quindi
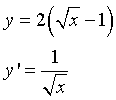
Il dominio dell'inversa è il codominio della funzione diretta, cioè [0;1]. L'inversa non è derivabile per x=0. Il suo grafico è simmetrico della diretta rispetto all'origine.
L'equazione dell'arco di parabola Γ1 è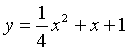 
Per il teorema di Archimede l'area S di un segmento parabolico di equazione 
di estremi
A e B è data da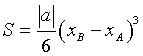 
, quindi l'area del segmento parabolico delimitato
da Γ1 è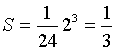 
.
L'area del secondo quadrante delimitata da Γ1 e dagli assi si ottiene sottraendo S dall'area di un triangolo rettangolo di cateti di misure 2 e 1, quindi è 2/3. Perché la retta di equazione x=k la divida in parti equivalenti bisogna che
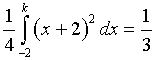
Per risolvere questa equazione conviene operare la sostituzione di variabile 
ottenendo
