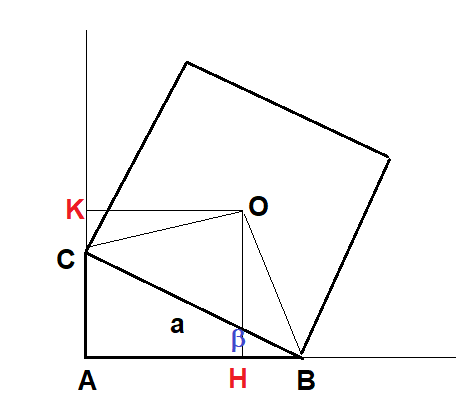
Dette H e K le proiezioni di O sulle rette dei cateti e detta β la misura dell'angolo acuto in B, l'angolo OCK ha misura
I triangoli rettangoli OBH e OCK aventi uguali l'ipotenusa e un angolo acuto sono congruenti. In particolare lo sono i cateti OH e OK.
Indicando con P(n) la probabilità di ottenere n e posto P(1)=x si ha
e quindi
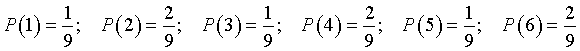
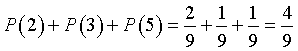
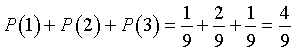
L'equazione della superficie sferica di centro C è 
Le equazioni parametriche della retta r sono
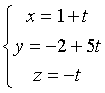
Le intersezioni tra retta e superficie sono date dall'equazione
La tangenza implica che il discriminante di questa equazione sia nullo
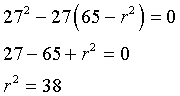
Quindi l'equazione della superficie sferica di centro C tangente alla retta r è
Indicando con x la misura del lato della base del parallelepipedo e con h la sua altezza si ha
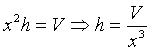
Indicando con a(x) la misura dell'area totale in funzione di x e assunto ovviamente x>0, si ha
L'area laterale risulta minima se il parallelepipedo è un cubo.
Indicando con d(x) la misura della diagonale del parallelepipedo si ha
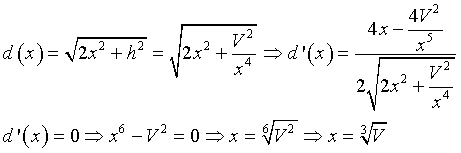
La diagonale risulta minima se il parallelepipedo è un cubo.
Il grafico dell'equazione 
è una semicirconferenza con centro
nell'origine, di raggio 5, compresa nel primo e secondo quadrante. Il suo punto P di ascissa 3 ha ordinata 4. La tangente in esso è perpendicolare alla retta di equazione
y=4/3x e quindi ha coefficiente angolare -3/4. La sua equazione risulta
Il coefficiente angolare della tangente ad una curva è dato dalla derivata della sua equazione.
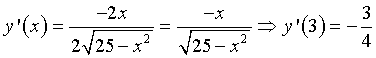
Si riconferma il risultato già trovato.
Per x→0 il numeratore e il denominatore della frazione 
tendono entrambi a 0 e il limite si presenta com indeterminato. Applicando il teorema di De L'Hôpital si ha
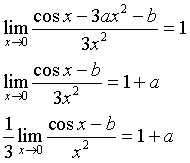
Il limite della frazione non diverge solo se b=1, nel qual caso il limite è indeterminato e si può nuovamente applicare il teorema di De L'Hôpital.
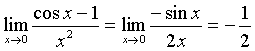
In definitiva si ottiene
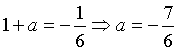
Il limite della funzione per x→0 da sinistra è -1. Perché la funzione sia derivabile, bisogna che sia continua in 0, quindi anche il limite da sinistra deve essere -1, cioè b=-1. La funzione è ovviamente derivabile per ogni x≠0. Perché la funzione sia derivabile anche per x=0, la derivata destra e quella sinistra devono coincidere. Si ha
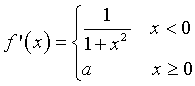
Il limite della derivata per x→0 da sinistra è 1. Il limite della derivata per x→0 da destra deve essere uguale, quindi a=1.
arctan(x) e x-1 sono crescenti su tutto l'insieme ℜ dei reali, quindi anche f(x) è crescente in ℜ e non esiste nessun intervallo di ℜ agli estremi del quale f(x) assuma valori uguali.
La funzione polinomiale fa(x) è continua e derivabile su tutto ℜ. Per x→-∞, fa(x)→-∞; per x→+∞, fa(x)→+∞.
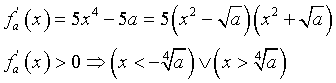
fa(x) ha un massimo relativo di valore 
per 
e un minimo relativo di valore
per 
