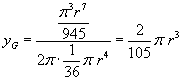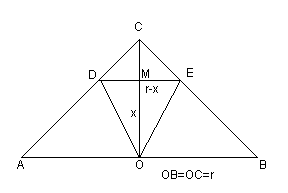
Rappresentando una sezione piana (passante per l'altezza del cono C) della figura si ha

Il volume del cono C' in funzione della sua altezza risulta
![]()
![]()
cresce in ]0 ; r/3[, cala in ]r/3 ; r[, si annulla in r/3.
Il volume di C' ha un massimo assoluto
![]()
La derivata seconda
![]()
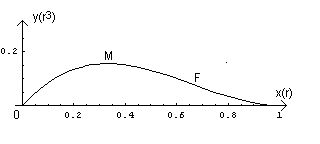
è negativa in ]0 ; 2/3 r[, positiva in ]2/3 r ; r[, nulla in 2/3 r. Il grafico ha un flesso obliquo
![]()
Grafico
Il valor medio del volume è dato da
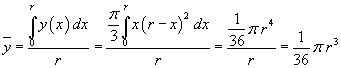
Il rapporto tra questo valore e il valore massimo del volume calcolato nel quesito precedente risulta quindi
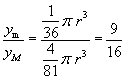
Il centro Z del cerchio inscritto nel triangolo C si può ottenere intersecando le bisettrici degli angoli ACB e CAB.
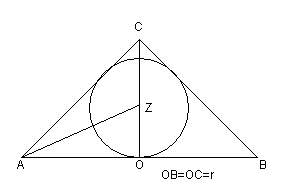
Il raggio ZO del cerchio inscritto (che coincide con il raggio della sfera S inscritta nel cono ABC) è dato da
![]()
Il volume della sfera inscritta risulta dunque
![]()
e il rapporto richiesto è
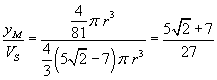
Il volume di rotazione richiesto è dato da
![]()
L'ordinata del baricentro, applicando inversamente il teorema di Guldino, può essere determinata dividendo il volume di rotazione per la superficie delimita dalla curva moltiplicata per 2 π