Indicando con P(A|A) la probabilità condizionata che un titolo aumenti dopo essere aumentato il giorno prima, con P(C|A) la probabilità condizionata che un titolo cali dopo essere aumentato il giorno prima, e con P(C|C) e P(A|C) gli altri casi analoghi si ha la seguente tabella
| P(A|A) | 0.60 |
| P(C|A) | 0.40 |
| P(C|C) | 0.70 |
| P(A|C) | 0.30 |
La probabilità che dopodomani il titolo aumenti è data dalla probabilità totale che
In definitiva la probabilità richiesta è
![]()
Il quadrato è sottoposto ad una rotazione di matrice
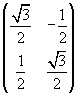
che trasforma il vettore B nel vettore B'
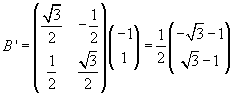
Supponendo ovviamente il quadrato rigido, non solo il centro, ma tutti i punti del quadrato sono sottoposti, dopo la rotazione, alla traslazione di vettore B'. La rototraslazione trasforma il vettore A nel vettore A''
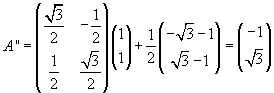
La serie 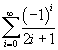 è assolutamente
convergente. Infatti si tratta di una serie a termini alternati
di tipo
è assolutamente
convergente. Infatti si tratta di una serie a termini alternati
di tipo ![]() in cui ui
è sempre positivo, ui+1 ≤ ui e
ui→0 per i→∞.
in cui ui
è sempre positivo, ui+1 ≤ ui e
ui→0 per i→∞.
La serie proposta si ottiene dallo sviluppo in serie di McLaurin dell'arcotangente circolare
![]()
per x=1: converge quindi a π/4 ed è nota come serie di Leibniz
Scrivendo l'equazione nella forma ![]() e graficando separatamente i due
membri si osserva che i due grafici si incontrano in un unico
punto del primo quadrante di ascissa maggiore di 1
e graficando separatamente i due
membri si osserva che i due grafici si incontrano in un unico
punto del primo quadrante di ascissa maggiore di 1
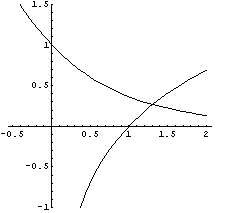
Applicando, ad esempio il metodo delle tangenti, si ottiene la definizione ricorsiva di una successione che converge alla soluzione dell'equazione proposta.
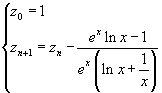
Usando una calcolatrice tascabile si ottengono i seguenti valori
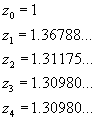
Una possibile implementazione in Javascript della procedura di calcolo della soluzione per qualunque k positivo è la seguente
function Soluzione(k,eps)
{
k = parseFloat(k);
eps = parseFloat(eps);
var z1;
var z2 = 1;
do
{
z1 = z2;
z2 = z2-(Math.exp(z2)*Math.log(z2)-k)/(Math.exp(z2)*(Math.log(z2)+1/z2));
} while (Math.abs(z2-z1)>eps)
return z2;
}
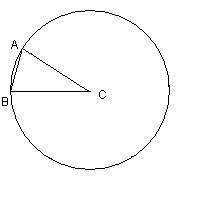
L'angolo al centro ACB che insiste sul lato AB del dodecagono
regolare inscritto in una circonferenza misura π/6; indicando
con r la misura del raggio della circonferenza
circoscritta, r è anche la misura dei lati obliqui del
triangolo isoscele ABC, la cui area è quindi
![]()
L'area del settore circolare ABC è 1/12 dell'area del cerchio. Il rapporto tra l'area del cerchio e quella del dodecagono inscritto è uguale al rapporto tra l'area del settore e l'area del triangolo, quindi
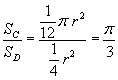
Scrivendo l'equazione assegnata nella forma equivalente
![]() e graficando separatamente le
funzioni a primo e a secondo membro, si ottengono la nota curva
logaritmica e l'iperbole equilatera di asintoti x=1 e
y=1. L'iperbole interseca la curva logaritmica in un punto
compreso tra 0 e 1 con ordinata negativa e in un punto di ascissa
maggiore di 1 e ordinata maggiore di 1.
e graficando separatamente le
funzioni a primo e a secondo membro, si ottengono la nota curva
logaritmica e l'iperbole equilatera di asintoti x=1 e
y=1. L'iperbole interseca la curva logaritmica in un punto
compreso tra 0 e 1 con ordinata negativa e in un punto di ascissa
maggiore di 1 e ordinata maggiore di 1.
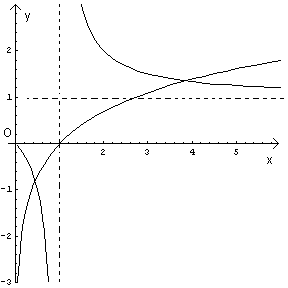
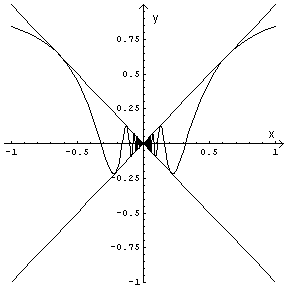
La funzione ![]() ha una
singolarità per x=0 ed è una funzione pari, quindi il suo grafico
nel piano Oxy è simmetrico rispetto all'asse delle ordinate e se
ne può capire l'andamento limitandosi a considerare le ascisse
positive. Poiché la funzione seno assume valori solo
nell'intervallo [-1;1] i valori di f(x) sono sempre
compresi nell'intervallo [-x,x]. In particolare, per il teorema
del confronto, per x→0, f(x) →0.
ha una
singolarità per x=0 ed è una funzione pari, quindi il suo grafico
nel piano Oxy è simmetrico rispetto all'asse delle ordinate e se
ne può capire l'andamento limitandosi a considerare le ascisse
positive. Poiché la funzione seno assume valori solo
nell'intervallo [-1;1] i valori di f(x) sono sempre
compresi nell'intervallo [-x,x]. In particolare, per il teorema
del confronto, per x→0, f(x) →0.
Questa conclusione può essere ulteriormente corroborata operando la sostituzione di variabile t = 1/x
![]()
La singolarità per x=0 è una singolarità eliminabile.
Si ha anche
![]()
Dato che il seno è sempre minore o uguale all'arco, la f(x) è sempre minore di 1 e non ha un massimo assoluto.
Il grafico di f(x) risulta tangente a una delle bisettrici dei quadranti quando
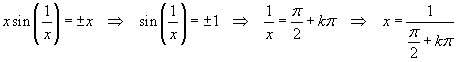
L'ultima tangenza si ha per x=2/π la tangenza
immediatamente precedente si ha per ![]()
Il minimo assoluto è quello di ascissa più prossima a
xT e può essere individuato azzerando la derivata
prima di f(x) ![]()
Per x≠0 si ottiene
![]()
Approssimando la soluzione dell'equazione in t con un metodo numerico si ottiene
![]()
In definitiva, il codominio della funzione risulta [fmin ; 1[.
Ricorrendo alla sostituzione di variabile
![]() , valida nel dominio di
integrazione, si ottiene
, valida nel dominio di
integrazione, si ottiene
![]()
e l'equazione assegnata può essere scritta
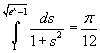
Una primitiva della funzione integranda è l'arcotangente, quindi
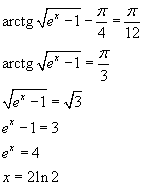
Una retta di equazione y=mx+p è un asintoto della
funzione f(x) in un intorno di ∞ se
![]()
Se m=0, l'asintoto si dice orizzontale, altrimenti si dice obliquo.
Una retta di equazione x=k si dice asintoto verticale di f(x) se per x=k la funzione ha una singolarità di seconda specie.
La funzione f(x) assegnata è dispari: il suo grafico è simmetrico rispetto all'origine.
f(x) ha due singolarità di seconda specie per x = ±1/2 e quindi due asintoti verticali.
Per x→∞ il fattore esponenziale converge a 1,
mentre l'altro diverge, dunque la funzione diverge e si può
vedere se ammette asintoti obliqui. Perchè questi possano
esistere bisogna (ma non basta) che converga il limite
![]() . Si ha
. Si ha
![]()
Per la determinazione del termine noto della retta conviene diversificare l'espressione della f(x) per argomenti positivi o negativi. Per argomenti positivi si ha
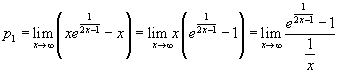
Applicando il teorema di De L'Hôpital si ottiene
![]() .
.
In modo analogo, per x→-∞ si ottiene
![]() .
.
In definitiva la f(x) ammette gli asintoti obliqui
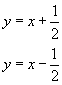
L'integrale indefinito della funzione y(x) si può ottenere integrando ripetutamente per parti
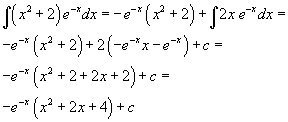
L'area richiesta è data da
![]()