Quesito 2

(a cura di Roberto Bigoni)

1. Considerando le prime due equazioni, si osserva che se k = 1 esse coincidono e il sistema è equivalente a quello formato dalle sole equazioni

   

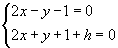
   che ha soluzioni

   

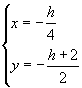
   Quindi, se k = 1, il sistema ammette una sola soluzione per ogni valore di h.

   Se invece k ≠ 1, le prime due equazioni possono essere interpretate come le generatrici di un fascio proprio di centro C(0; -1): il sistema ammette una soluzione solo se anche la terza equazione rappresenta una retta passante per C, cioè se h = 0.

   Il quesito può essere risolto in modo più formale applicando il teorema di Rouché-Capelli: per ogni k la matrice incompleta del sistema

   

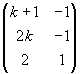
   ha rango 2.

   Quindi perché il sistema ammetta soluzione, bisogna che anche la matrice completa

   

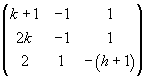
   abbia rango 2 per ogni k, cioè che il suo determinante h(1-k) sia uguale a 0, da cui h=0.

   Se però k=1, la matrice completa ha rango 2 per qualunque valore di h e il sistema è comunque determinato.

    

2. Se k = 1, le rette r e s coincidono, hanno coefficiente angolare 2; la retta t, di coefficiente angolare -2 le interseca.

   Se k ≠ 1, le tre rette passano per C; in particolare la retta t ha equazione

   

    

    

3. Perché le tre rette individuino un triangolo, è necessario che k ≠ 1 (altrimenti r e s coincidono) e che h ≠ 0 (altrimenti tutte e tre le rette passano per lo stesso punto.

   Vanno inoltre esclusi il parallelismo tra r e t e il parallelismo tra s e t.

   

    

    

4. Si è già visto che, per k ≠ 1, le rette r e s si intersecano in C(0; -1).

   Intersezione r/t

   

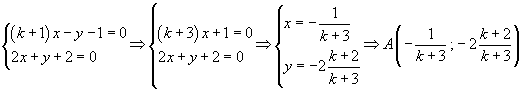
   Intersezione s/t

   

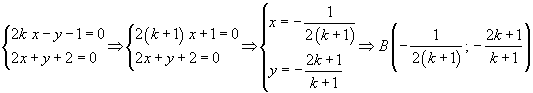
   L'area del triangolo di vertici A, B, C è data dalla metà del valore assoluto del determinante

   

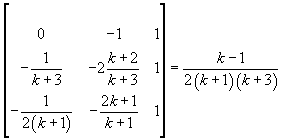
   Si ottiene quindi

   

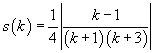
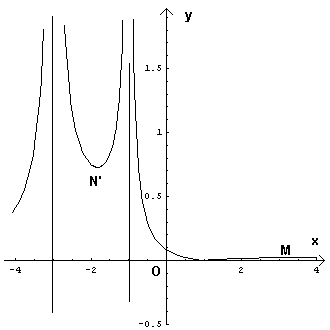
   Per ottenere nel modo più rapido la curva di equazione s(k) conviene studiare la curva di equazione

   

   e sostituire poi gli archi di ordinata negativa con i simmetrici rispetto all'asse delle ascisse.

   • S(x) è definita per k ≠ -1 e k ≠ -3,

     è positiva in

     

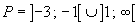
     negativa in

     

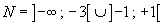
     nulla per x = 1.

   • Asintoto orizzontale: asse delle ascisse

     Asintoti verticali: x = -3 e x = -1.

   • Pendenza

     

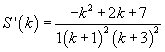
     Il denominatore nel dominio è sempre positivo, dunque il segno coincide con quello del numeratore. Gli zeri del trinomio numeratore sono 1 ± 2√2, quindi la derivata, nel dominio, è crescente in

     

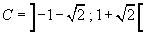
     decrescente in

     

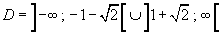
     S(x) ha un minimo relativo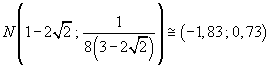

     

     e un massimo relativo

     

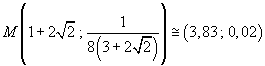
   I risultati ottenuti sono sufficienti per tracciare il grafico di S(x).

   

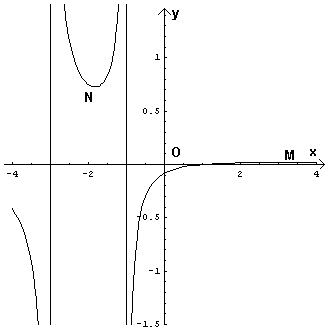
   Per s(x) si ha quindi