La probabilitÓ che una variabile casuale x assuma un valore compreso nell'intervallo
![]()
pu˛ essere desunta dalla tabella calcolando la differenza
tra i valori corrispondenti rispettivamente a
+1,25 e 1,25. La probabilitÓ
pL che una barra abbia lunghezza
accettabile risulta quindi
![]()
Analogamente la probabilitÓ che una variabile casuale x assuma un valore compreso nell'intervallo
![]()
pu˛ essere desunta dalla tabella calcolando la differenza
tra i valori corrispondenti rispettivamente a
+1,50 e 1,50. La probabilitÓ
pD che una barra abbia diametro
accettabile risulta quindi
![]()
La probabilitÓ pV che una barra
sia vendibile Ŕ data dal prodotto di
pL e pD:
![]()
La probabilitÓ che, su n barre prodotte,
k siano vendibili Ŕ binomiale (bernoulliana),
quindi su n barre prodotte mediamente sono
vendibili
![]()
barre, con una devianza
![]()
Per il teorema di BienaymÚ-Cebycev, la probabilitÓ che un
dato x si discosti dalla media non meno di uno
scarto ξ non supera il rapporto tra la devianza e il
quadrato dello scarto stesso. Nel caso in questione lo scarto
considerato Ŕ il 5% del numero delle barre
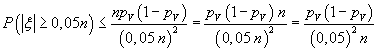
Questo valore deve essere il 5%, quindi
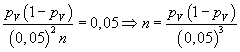
Per n = 2000 e pV =
0,68 il valor medio teorico del numero di barre
vendibili Ŕ n pV = 1360, quindi una
frequenza f = 1000 ha uno scarto ξ =
360.
Riprendendo il teorema di BienaymÚ-Cebycev, la probabilitÓ di avere uno scarto ξ ≥ 360 non supera il rapporto tra la devianza e il quadrato dello scarto stesso.
![]()
Quindi per pV = 0,68, la frequenza
f = 1000 Ŕ altamente improbabile e bisogna
valutare l'ipotesi di malfunzionamenti nel processo di
produzione.
L'evento richiesto si verifica se per n-1
volte si ha una barra non vendibile e infine una barra
vendibile; per il principio della probabilitÓ composta
![]()
Si propone una funzione Javascript per il calcolo di
P(p,n)
function funzione(p,n)
{
if ((p≤0)||(p≥1)||(n<1)) return 0;
result = p;
if (n>1)
{
q = 1-p;
for (i=1; i< n; i++) result *= q;
}
return result;
}