Sia AB un segmento di lunghezza 2a e C il suo punto medio.
Fissato un conveniente sistema di coordinate cartesiane monometriche (x,y):
a) si verifichi che il luogo dei punti P tali che
![]()
(k costante positiva assegnata) è una circonferenza (circonferenza di Apollonio) e si trovi il valore di k per cui la soluzione degenera in una retta;
b) si determini il luogo geometrico γ dei punti X che vedono AC sotto un angolo di 45°;
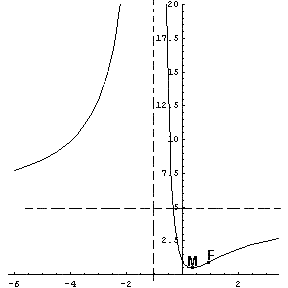
c) posto X, appartenente a γ, in uno dei due semipiani di origine la retta per A e per B e indicato con α l'angolo XAC si illustri l'andamento della funzione y = f(x) con f(x) = (XB / XA)2 e x = tg α.
a)
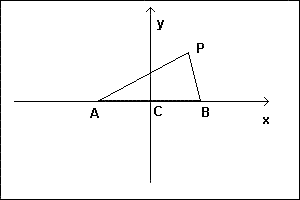
Scegliendo come origine del sistema di riferimento il punto medio C e come asse delle ascisse la retta AB si ha
A(-a;0) e B(a;0)
![]()
![]()
Il luogo richiesto nel punto a) risulta
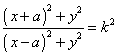
Sviluppando, raccogliendo e ordinando si ottiene
![]()
che risulta l'equazione di una circonferenza di centro
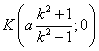
e raggio
![]()
Per k→1 il raggio tende all'infinito e quindi la circonferenza tende ad una retta.
b)
Il luogo γ è il maggiore degli archi di estremi AC della circonferenza circocritta al quadrato di lato AC.
È possibile situare questo arco nel semipiano delle ordinate positive o nel semipiano delle ordinate negative.
Nel primo caso l'equazione della circonferenza si ottiene dal centro
![]()
e dal raggio
![]()
L'equazione del luogo è quindi
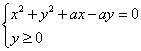
Nel secondo caso l'equazione della circonferenza si ottiene dal centro
![]()
e dal raggio
![]()
L'equazione del luogo è quindi
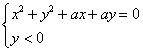
c)
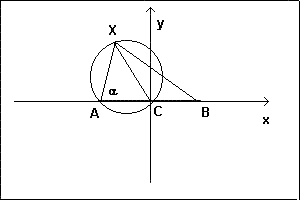
Per il teorema dei seni
![]()
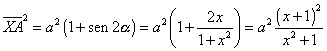
Ancora per il teorema dei seni
![]()
Per il teorema del coseno
![]()
![]()
![]()
![]()
e con le formule parametriche
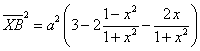
In definitiva si ottiene
![]()
La funzione f(x) richiesta risulta
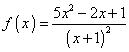
La f(x) è definita per ogni x reale diverso da -1 ed è sempre positiva.
Interseca l'asse delle ordinate nel punto (0;1).
Per x → -1 tende
a ∞ (asintoto verticale);
per x → ∞
tende a 5 (asintoto orizzontale).
La derivata prima è
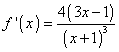
positiva per x>1/3, dove si ha un minimo M(1/3;1/2)
La derivata seconda risulta
![]()
positiva per x>1; flesso obliquo in F(1;1)