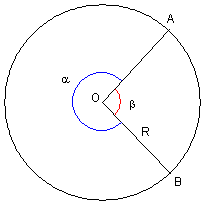

Indicando con α la misura in radianti dell'ampiezza di uno degli angoli AOB e con β quella dell'altro, e con lα e lβ le misure degli archi corrispondenti, si ha immediatamente
![]()
Da lα si ottiene la misura del raggio di base del cono corrispondente
![]()
L'apotema del cono coincide con il raggio R del cerchio dato. L'altezza del cono si ricava con il teorema di Pitagora.
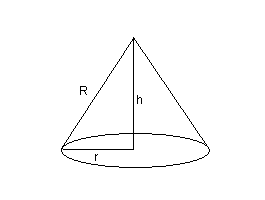
![]()
Il volume del cono è un terzo dell'area di base per l'altezza
![]()
Per massimizzare il volume è sufficiente massimizzare il numeratore; tale derivata risulta
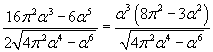
Per α positivi e minori di un giro questa funzione cresce in
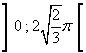
per poi calare. Dunque il volume risulta massimo per
![]()
L'arco corrispondente vale ovviamente
![]()
L'area del settore è
![]()
L'area del cerchio è π m2; il rapporto tra le aree è dato dal radicale il cui valore, espresso in percentuale, risulta circa 81,65%
Il volume massimo risulta
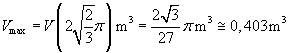
Il volume dell'altro cono risulta
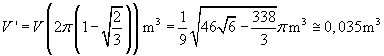
Ogni metro cubo vale 1000 litri. La capacità chieste sono rispettivamente di circa 403 e 35 litri per un totale di 438 litri.
Il seno del semiangolo θ di apertura del cono coincide numericamente con la misura del raggio di base. Si ha
![]()
e quindi
![]()
Raddoppiando si ottiene per l'apertura 109°28'16''.
Questi valori sono stati ottenuti direttamente con l'uso delle funzioni inverse di una calcolatrice scientifica. Dovendo risolvere l'equazione
![]()
senza l'uso delle funzioni inverse, si può, ad esempio, applicare il metodo delle tangenti, applicato alla approssimazione dello zero della funzione f(x) nell'intervallo assegnato
![]()
La funzione sen(x) nel primo quadrante ha concavità negativa: ciò vale anche per la funzione f(x).
La funzione f(x) è negativa nell'estremo inferiore a=0, dunque x0=a=0
Applicando la ricorsione
![]()
si ottengono le successive approssimazioni
| xi | valore |
|---|---|
| x1 | 0,816497 |
| x2 | 0,944633 |
| x3 | 0,955238 |
| x4 | 0,955317 |
| x5 | 0,955317 |
Osservando che l'approssimazione, con precisione al milionesimo, si stabilizza sul valore 0,955317 si può assumere questo valore come stima soddisfacente dell'arcoseno.