,
positiva per x negative e viceversa. γ cresce per x
negative, cala per x positive, ha un massimo assoluto in
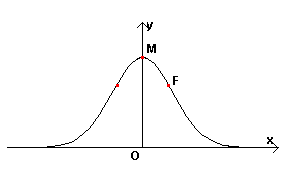
M(0;k)La derivata seconda è 
.
Il segno è quello del binomio:
γ ha concavità positiva dove il binomio è positivo e
viceversa e ammette flessi obliqui 
Data la simmetria di γ è sufficiente massimizzare il rettangolo con un vertice P sul ramo di γ del primo quadrante e lati paralleli agli assi.
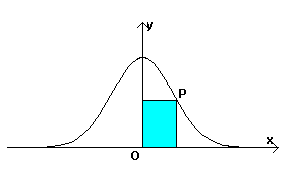
Detta x l'ascissa di P, l'area del rettangolo risulta
La derivata prima rispetto a x è
che risulta positiva in
Il rettangolo ha area massima se ha vertici nei punti di flesso F.
L'equazione da risolvere è
Con la sostituzione 
,
l'equazione diventa
Con il passaggio precedente si è ottenuta l'equazione
che rappresenta una distribuzione normale di probabilità di media μ=0 e deviazione standard σ=1. La più generale espressione di una distribuzione normale di probabilità è data dalla funzione
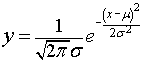
(vedere distribuzioni continue di probabilità)
Una media diversa da zero implica una traslazione dell'asse di simmetria della curva, una deviazione standard diversa da 1 implica una variazione della posizione dei flessi rispetto all'asse di simmetria.