di angolo
piatto. di angolo
piatto.Indicando con R il raggio della sfera, la superficie
della stessa è 
. Il cilindro
equilatero inscritto ha altezza 
e raggio di base
e la sua superficie totale è
Il rapporto richiesto è immediato.
Per rispondere al quesito è sufficiente pensare allo spigolo di un cubo che, nella similitudine indicata, triplica: la superficie totale diviene 9 volte maggiore e il volume 27 volte maggiore.
Il problema è risolto dal calcolo delle disposizioni con ripetizione di 3 elementi a gruppi di 4: D'3,4=34.
La funzione cercata deve avere una singolarità a salto limitato (prima specie) per x=2. La si può definire nel seguente modo
Sono comunque ammissibili tutte le situazioni dello stesso tipo.
Rispondono ai requisiti tutte le funzioni che hanno derivata positiva
nell'intervallo ]-1;1[, negativa in ]-∞;-1[U]1;+∞[,
nulla in ±1. L'esempio più diretto è dato da
.
La primitiva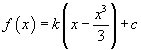 
deve essere
soddisfatta dalle coppie fornite dal testo:
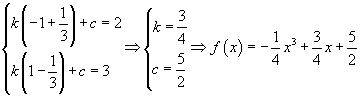
Sono comunque accettabili anche tutte le funzioni deducibili con omotetie e traslazioni da una funzione dispari in cui un minimo relativo sia seguito da un massimo relativo. Ad esempio
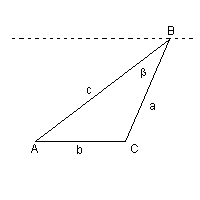
Indicando con B il vertice opposto alla base AC di misura assegnata b, dato che l'area deve essere costante, pure l'altezza relativa ad AC deve essere costante e B deve giacere su una retta parallela alla base. Detto β l'angolo con vertice in B, β può variare solo nell'intervallo ]0;βmax] dove con βmax si indica il valore di β per cui il triangolo ABC è simmetrico rispetto all'asse della base AB, cioè il valore per cui il triangolo ABC è isoscele.
Per il teorema del coseno si ha
da cui
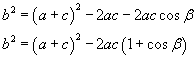
Ricordando ancora che l'area del triangolo è data da
si ottiene
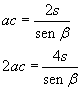
e quindi
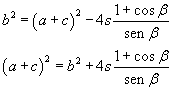
Perché il perimetro sia minimo bisogna che la somma a+c sia minima e, dato che tale somma è intrinsecamente positiva, bisogna che lo sia anche il suo quadrato.
Posto 
si ha
Questa derivata è sempre negativa, f(β) è decrescente in tutto il suo dominio ed ha un minimo nell'estremo destro del dominio, cioè per βmax. Di conseguenza il perimetro è minimo quando il triangolo è isoscele.
Deve essere
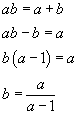
Escludendo a=1, che annulla il denominatore, e a=2, che produce b=a, per ogni altro valore arbitrario di a si ottiene una coppia che soddisfa la richiesta.
Scrivendo l'equazione nella forma 
e graficando separatamente i due
membri si ha
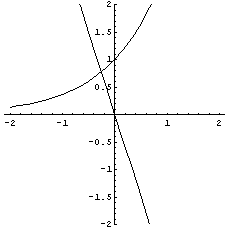
L'esponenziale sempre crescente la retta sempre decrescente si intersecano in un sol punto, con ascissa localizzabile tra -1 e 0.
Per approssimare questa ascissa si può procedere con il metodo delle tangenti
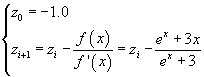
Si ottiene la successione
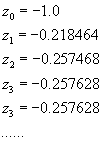
E una trasformazione lineare di matrice
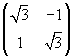
equivalente al prodotto
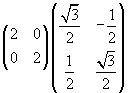
Si tratta quindi di una similitudine di centro O, risultante dalla composizione di una omotetia di rapporto 2 con una rotazione antioraria di 30°.