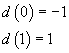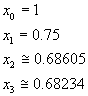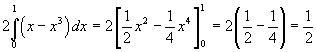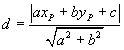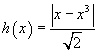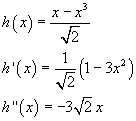Problema 2
Quesito 1
Quesito 2
Assumendo 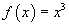 , per le considerazioni
precedenti, f(x) è non decrescente su tutto r mentre y(x) è crescente: le curve non possono
intersecarsi che in un solo punto.
, per le considerazioni
precedenti, f(x) è non decrescente su tutto r mentre y(x) è crescente: le curve non possono
intersecarsi che in un solo punto.
L'ascissa dell'intersezione si ottiene determinando lo zero della funzione differenza
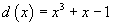 . Poiché
. Poiché
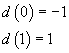
per il teorema di Bolzano lo zero è comprezo tra 0 e 1 e può essere approssimato con il metodo delle tangenti assumendo
1 come valore iniziale (per x=0 d(x) ha un flesso) e
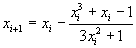 . Si ottiene
. Si ottiene
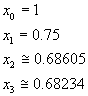
Quesito 3
La funzione f(x) è non decrescente in tutto il dominio e quindi invertibile su tutto il dominio. La funzione
inversa è
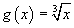 il cui grafico è simmetrico di quello
di f(x) rispetto alla bisettrice del primo quadrante.
il cui grafico è simmetrico di quello
di f(x) rispetto alla bisettrice del primo quadrante.
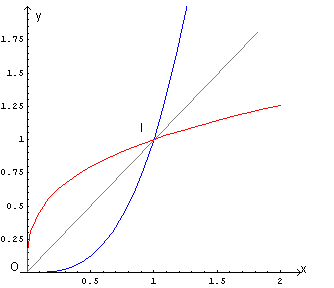
Limitandosi al primo quadrante, le due curve si intersecano nell'origine e nel punto I(1;1). L'area da esse
delimitata può essere calcolata raddoppiando l'area delimitata dalla bisettrice e da f(x), cioè calcolando
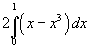
Si ottiene
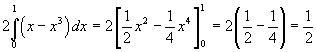
Quesito 4
Dato che le sezioni sono rettangoli di uguale altezza, la loro area è proporzionale alla loro base, che è data dal
doppio della distanza PH di un punto P di γ dalla bisettrice del quadrante e quindi, in ultima analisi, è
funzione solo di tale distanza per cui è sufficiente massimizzare tale distanza (figura).
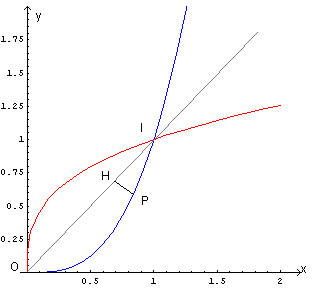
Ricordando che la distanza di un punto P(xP;yP) dalla retta di equazione ax+by+c=0
è espressa da
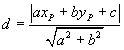
la funzione da massimizzare è
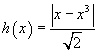
Per 0<x<1 si ha più semplicemente
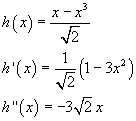
Per 0<x<1 la derivata prima si annulla per 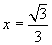 ,
valore per cui la derivata seconda è negativa e quindi valore massimante.
,
valore per cui la derivata seconda è negativa e quindi valore massimante.
Il massimo dell'area è
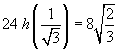
Il volume di W si ottiene semplicemente moltiplicando l'area di base calcolata nel quesito 3 per l'altezza (12)
e risulta 6.
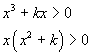
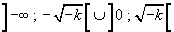 , positiva in
, positiva in
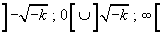 , nulla in
, nulla in
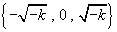 .
.![]()
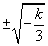 , quindi decresce
nell'intervallo delimitato dagli zeri, cresce esternamente a tale intervallo, ha un massimo relativo nel
primo zero e un minimo relativo nel secondo.
, quindi decresce
nell'intervallo delimitato dagli zeri, cresce esternamente a tale intervallo, ha un massimo relativo nel
primo zero e un minimo relativo nel secondo.![]()